| 俙侾俋丂丂俹俤俼俿朄 搘椡栚昗 丂丂棟夝偡傞 媄弍巑帋尡偺栤戣偐傜偼昁梫嵟彫尷偺堷梡偵偲偳傔傞丅乮栤戣乯偑婰偝傟偰偄傞晹暘偼偦偺堷梡偱偁傞丅 栤戣偍傛傃夝摎偼擔杮媄弍巑夛偺儂乕儉儁乕僕傛傝昁梫偵墳偠偰擖庤偟偰偔偩偝偄丅 丂丂媄弍巑戞堦師帋尡偺栤戣丂丂丂丂 栤戣斣崋偑愒帤偺傕偺偼丄儃乕僫僗栤戣 俫俀俉擭丂嘥亅侾亅係丂丂丂俫俀俆擭丂嘥亅侾亅係丂丂丂俫俀俁擭丂嘥亅侾亅俁 俫俀俉擭丂嘥亅侾亅係 惓摎丗丂嘋丂 乮夝摎乯 夝摎丗嘋 暋嶨側岺掱偲擔悢偑帵偝傟偰偄傞偑丄奺儖乕僩偺昁梫擔悢傪摢偐傜愊傒忋偘偰偄偗偽摎偊偵摓払偱偒傞丅偨偲偊偽拞墰偵偁傞億僀儞僩嘐偱偼丄儖乕僩倫亅倐侾偱偼俀俆擔昁梫偱偁傞偑丄倫亅倎侾亅倎俀亅僟儈乕偱偼俁俁擔偲挿偔偐偐傞丅廬偭偰丄儖乕僩倫亅倐侾偺岺掱偼梋桾傪帩偭偰偄傞偙偲偑傢偐傞丅弅傔傞偲偡傟偽丄岺掱倫亅倎侾亅倎俀亅僟儈乕偺偳偙偐偱偁傞丅摨偠傛偆偵擔悢偺愊傒忋偘傪峴偭偰峴偗偽丄偳偙偵弅傔偟傠偑偁傞偐偑傢偐傞丅 側偍丄僟儈乕偲偼丄岺掱倎俀偑廔椆偟偰億僀儞僩嘊偵摓払偟側偄偲億僀儞僩嘐偐傜偺岺掱倐俀偑奐巒偱偒側偄偙偲傪帵偡婰崋偱偁傞丅 壓偺恾偵帵偡傛偆偵丄嶌嬈偺恑峴弴偵昁梫擔悢傪媮傔偰偄偔偲丄仜偱埻傫偩儖乕僩乮倫亅倎侾亅倎俀亅僟儈乕亅倐俀亅倐俁亅倖乯偑僋儕僥傿僇儖僷僗偲側傞丅 旓梡傪巟暐偭偰岺婜傪侾擔抁偔偡傞偲偡傞偲丄倎俀偐倐俁偺偳偪傜偐偱偁傞偑丄倐俁偺曽偑捛壛旓梡偑埨偄丅 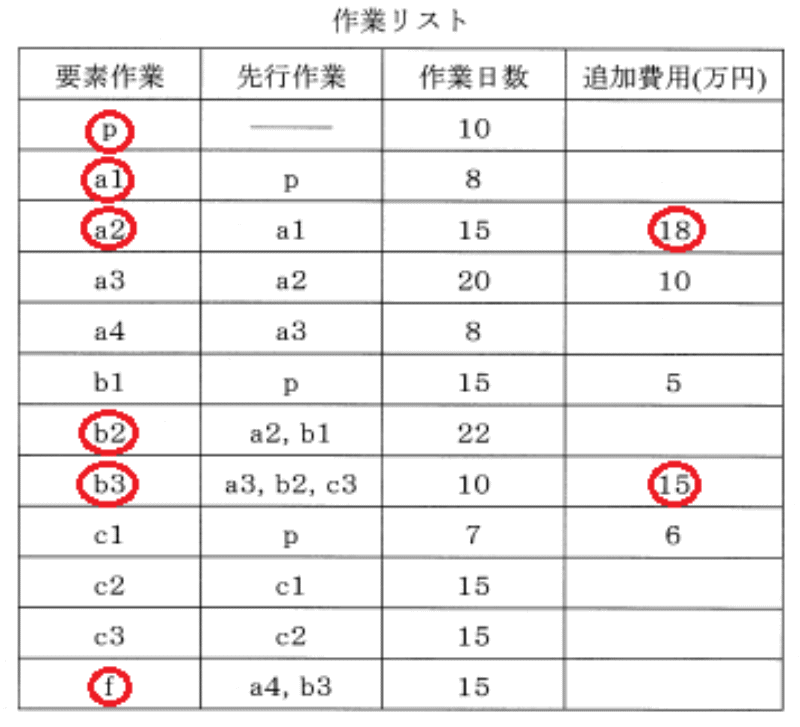 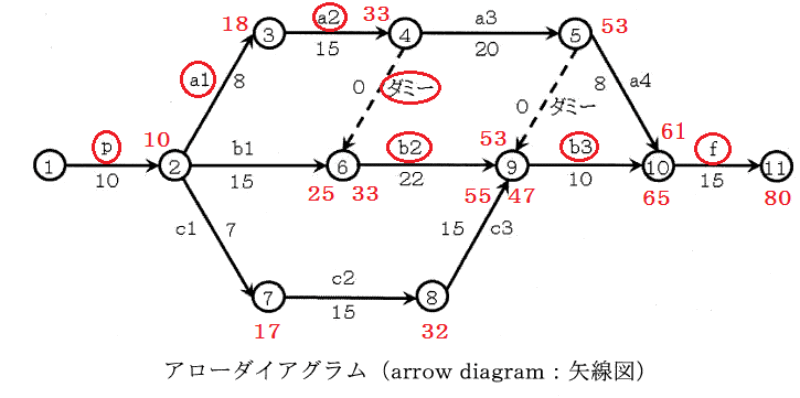 恾偺愢柧 僲乕僪俇 丂嘆傪弌敪偟偰嘐偺揰偵摓払偡傞偵偼丄 丂宱楬倫亅倐侾偱偼俀俆擔傪梫偡傞丅 丂宱楬倫亅倎侾亅倎俀亅僟儈乕偱偼俁俁擔傪梫偡傞丅 丂宱楬倫偼嫟捠偱偁傞偐傜丄宱楬倐侾偵乮俁俁亅俀俆乯亖俉擔偺梋桾偑偁傞丅 丂乮梋桾偑偁傞宱楬偼柍棟偟偰抁弅偟偰傕堄枴偑側偄乯 僲乕僪俋 丂嘆傪弌敪偟偰嘓偵摓払偡傞偵偼丄 丂嘐傪宱桼偟偰偔傞偲俆俆擔 丂嘍傪宱桼偟偰偔傞偲俆俁擔 丂嘒傪宱桼偟偰偔傞偲係俈擔 丂嘍傪宱桼偡傞宱楬偵俀擔丄嘒傪宱桼偡傞宱楬偵俉擔偺梋桾偑偁傞丅 丂乮梋桾偑偁傞宱楬偼柍棟偟偰抁弅偟偰傕堄枴偑側偄乯 僲乕僪侾侽 丂倎係偵係擔偺梋桾偑偁傞丅 丂乮梋桾偑偁傞宱楬偼柍棟偟偰抁弅偟偰傕堄枴偑側偄乯 俫俀俆擭丂嘥乕侾亅係 惓摎丗丂嘋丂 乮夝摎乯 丂宱楬丄俛仺俤仺俥乮偁仺偆仺偊仺偍仺偐乯偑嵟挿擔悢傪梫偡傞宱楬偱係亄係亄侽亄俆亖侾俁擔丅偙偺擔悢傪嵟彫旓梡偺搳擖偱侾擔抁偔偟偰侾俀擔偲偡傞丅俛丂係俆枩墌丄俤丂俆侽枩墌丄俥丂係侽枩墌偱偁傞偐傜俥偑堦斣埨偄丅 俫俀俁擭丂嘥乕侾亅俁 H俀俁擭搙栤戣丂 惓摎丗丂嘊丂 乮夝摎乯 傾儘乕僟僀儎僌儔儉偼俫俀俆擭嘥亅侾亅係偵摨偠丅俛丂係俆枩墌丄俤丂係侽枩墌丄俥丂俆侽枩墌偱偁傞偐傜俤偺係侽枩墌偑堦斣埨偄丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂栤戣堦棗昞傊栠傞 |