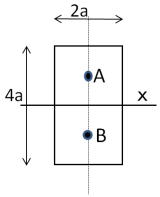
Ｃ１２　　慣性モーメント 努力目標 　　理解する 技術士試験の問題からは必要最小限の引用にとどめる。（問題）が記されている部分はその引用である。 問題および解答は日本技術士会のホームページより必要に応じて入手してください。 　　技術士第一次試験の問題　　　　　 問題番号が赤字のものは、ボーナス問題 Ｈ２７年　１－３－４ Ｈ２７年　１－３－４ 正答：　③ それぞれの軸を中心に回転させた時のモーメントは、重心点が回転中心からどの程度離れているかで、その大きさの大小関係は直感的に判断できると思います。結局は距離ですから、ピタゴラスの定理、ｚ２＝ｘ２＋ｙ２に関係することになります。 （解答） 慣性モーメントの大きさはＷｉｋｉｐｅｄｉａにあるように、質量×距離２である。 慣性モーメント（Ｗｉｋｉｐｅｄｉａ）  Ｘ軸の周りに回転  ｙ軸の周りに回転  ｚ軸の周りに回転 Ixは、質点Aと質点Bは共に４ａ２に比例し、ｘ軸からの距離はａである。今、比例定数をＫとすると、 Ｉｘ＝２×Ｋ×４ａ２×ａ２＝８Ｋａ４ 同じく、Ｉｙの質点Ａと質点Ｂは共に４ａ２に比例し、ｘ軸からの距離はａ／２である。 Ｉｙ＝２×Ｋ×４ａ２×（ｑ／２）２＝２Ｋａ４ Ｉｚの質点、Ａ、Ｂ、Ｃ、Ｄはすべて２ａ２であり、質点のｚ軸からの距離は√（（ａ／２）２＋ａ２）＝√（５）ａ／２である。従って、 Ｉｚ＝４×Ｋ×２ａ２×（√（５）ａ／２）２＝１０Ｋａ４ 従って、Ｉｘ＞Ｉｘ＞Ｉｙであり、Ｉｚ＝Ｉｘ＋Ｉｙとなっている。   　　　　　　　　　　　　　　　　問題一覧表へ戻る

～