| 令和元年度 技術士一次試験 基礎科目 解答 10月13日に実施、10月21日に公開されたその試験問題の解答を作成する。 なお、問題文は著作権の関係もあり、必要に応じて最小限の引用にとどめる。 技術士一次試験の目次一覧に戻る 書籍 技術士一次試験 基礎科目を極める(2022年版) 平成16年度~令和3年度 基礎科目の解答を収録 基礎科目について、 過去の問題と今回の問題比較 類似の問題が多数ありますので、やはり過去問をしっかりとやるということに尽きます。 各群より3問選択 合計で15問解答 内8問正解で基礎科目は合格 なお、日本技術士会が現在公開している平成16年~28年の過去問356題の解答は 技術士一次試験・基礎科目 H16年~28年の356全問解答集 にまとめて記しています。 令和元年度技術士一次試験 基礎科目 1群 Ⅰ-1-1 最適化問題 Ⅰ-1-2 年間在庫維持費用最小化問題 Ⅰ-1-3 製作図作成の基本 Ⅰ-1-4 材料の強度 Ⅰ-1-5 待ち行列問題 Ⅰ-1-6 人名のついた数式 2群 Ⅰ-2-1 基数変換 Ⅰ-2-2 二分探索木 Ⅰ-2-3 空間距離 Ⅰ-2-4 表現形式 Ⅰ-2-5 ハミング距離 Ⅰ-2-6 スタック 3群 Ⅰ-3-1 偏微分 Ⅰ-3-2 行列式 Ⅰ-3-3 物体の落下運動方程式 Ⅰ-3-4 ポアソン比 Ⅰ-3-5 ひずみエネルギー Ⅰ-3-6 剛体振り子の周期 4群 Ⅰ-4-1 ハロゲンとハロゲン化水素の性質 Ⅰ-4-2 同位体 Ⅰ-4-3 原子数比率を求める Ⅰ-4-4 知識を試す問題 Ⅰ-4-5 DNA二重らせん Ⅰ-4-6 タンパク質 5群 Ⅰ-5-1 大気汚染 Ⅰ-5-2 環境保全・環境管理 Ⅰ-5-3 長期エネルギー需給見通し Ⅰ-5-4 二酸化炭素発生量 Ⅰ-5-5 科学史 Ⅰ-5-6 特許法と知的財産基本法 (参考) 平成30年度問題より 技術士一次試験・基礎科目 H16年~28年の356全問解答集へ戻る R01年 基礎科目問題 解答 1群 設計・計画に関するもの R01年 基礎科目問題 トップに戻る Ⅰ-1-1 最適化問題 解答:⑤ (ア)誤 最適化問題において、目的関数が線型関数で、なおかつ線型関数の等式と不等式で制約条件が記述できる問題である。(Wikipedia) (イ)正 たとえば、平成28年度Ⅰ-1-5 生産個数最適化問題 (ウ)正 凸最適化とは最適化問題の分野のひとつで、凸集合上の凸関数の最小化問題である。 凸最小化問題は一般的な最適化問題よりも簡単に最適化が可能であり、局所的な最小値が大域的な最小値と一致する性質をもつ。(Wikipedia) (エ)正 整数計画問題は、線型計画問題において、解ベクトルxの各要素を整数に限定した問題をいう。これはNP困難な問題に該当する。線型計画問題には多項式時間アルゴリズムが存在するのに対し、整数計画問題には存在しない。(Wikipedia) ヒューリスティクス(英: heuristic, 独: Heuristik)または発見的(手法)とは、必ず正しい答えを導けるわけではないが、ある程度のレベルで正解に近い解を得ることができる方法である。発見的手法では、答えの精度が保証されない代わりに、回答に至るまでの時間が少ないという特徴がある。(Wikipedia) Ⅰ-1-2 年間在庫維持費用最小化問題 ボーナス問題 解答:② 題意より、年間総費用は、 年間総費用C(q)=d/q×k+q/2×h (円/年) C(q)の最小値を求めるには、C(q)をqで微分してゼロと置く。 C(q)/dq=-d/q2×k+1/2×h=0 求める発注量qは、 q=(2kd/h)0.5=60 答えは②の60単位である。 Ⅰ-1-3 製作図作成の基本 本問題は、平成29年度Ⅰ-1-5、平成26年度Ⅰ-1-6に同じ。 解答:⑤ (ア)誤 常識的に判断する。形状の幾何学的な公差の指示は必要である。 (イ)正 常識的に判断する。問題文通りである。 (ウ)正 量産される機械部品の仕上がり寸法を検査する測定器。あらかじめその部品の許容される寸法誤差範囲 (許容限界寸法) を定め,その上限と下限のゲージをつくっておき,製品寸法がこの大小2つのゲージの間にあるかどうか検査する。このゲージには穴および軸の寸法を検査する穴用限界ゲージと軸用限界ゲージがあり,プラグゲージとはさみゲージがそれぞれの代表例である。さらに穴・軸用のほかにねじ・テーパ用などの限界ゲージがある。また使用目的によって,工作用,検査用,点検用 (工作用,検査用ゲージの寸法検査に用いる) などに区別される。(コトバンク) (エ)誤 日本では図面は第三角法で描くとJISに規定されている。第二角法はない。 (オ)正 問題文の通りである。 Ⅰ-1-4 材料の強度 ボーナス問題である 解答:⑤ 特に説明を要さないと考えるが、座屈の意味のみを記す。 座屈は、構造物に加える荷重を次第に増加すると、ある荷重で急に変形の模様が変化し、大きなたわみを生ずることをいう[1]。構造に座屈現象を引き起こす荷重をその構造の座屈荷重という。(Wikipedia) Ⅰ-1-5 待ち行列問題 平成29年度Ⅰ-1-1、平成27年度Ⅰ-1-2に同じである。 解答:② 式に数値を当てはめていく。1時間あたりで考えると、 到着率=60人/時間 サービス率とは何かが分かりにくいが、次の式である。 サービス率=90人/時間 ((40秒/人)より) トラフィック密度(利用率)=到着率/サービス率=4/9 平均系内列長=トラフィック密度/(1-トラフィック密度)=0.8 平均系内滞在時間=0.8/40×3600=72秒 Ⅰ-1-6 人名のついた数式 解答:③ マクローリン展開、オイラーの等式は有名である。この2つを知っていれば解答③が出てくる。 ロピタルの定理は耳慣れないが、Wikipediaでは次のようになっている。 ロピタルの定理 (ロピタルのていり、英: l'Hôpital's rule) とは、微分積分学において不定形の極限を微分を用いて求めるための定理である。ベルヌーイの定理 (英語: Bernoulli's rule) と呼ばれることもある。本定理を (しばしば複数回) 適用することにより、不定形の式を非不定形の式に変換し、その極限値を容易に求めることができる可能性がある。(続く) 2群 情報・論理に関するもの R01年 基礎科目問題 トップに戻る Ⅰ-2-1 基数変換 解答:① わかっていれば簡単な問題である。 2進数は桁が上がるにつれて2倍、2倍となっていく。 2進数の1011.1は10進数では1×103+0×102+1×101+1×100+1×10-1=11.5である。 16進数の表記は、1から16までが、1,2,3,4,5,6,7,8,9、A,B,C,D,E,Fとなる。 Bは10進数では11に相当し、.8は10進数では8/16、すなわち0.5に相当する。 従って、16進数のB.8は10進数では11.5である。 Ⅰ-2-2 二分探索木 ボーナス問題? 関連問題 平成30年度Ⅰ-2-5 解答:① 難しそうに見えるが、ルールに従って数字を配列していけば、答えは容易に見つかる。  Ⅰ-2-3 空間距離 解答:③ この問題はひらめきが問われる。ひらめけば一瞬にして答えに至る。 文書D/文書Aで、単語1=21/7=3、同じく単語2=9/3=3、単語3=6/2=3 Ⅰ-2-4 表現形式 解答:③ 数値の定義より、数値には小数が許される。②.52や③-.37は小数である。 小数の定義には符号が含まれていないので、小数に+や-が付くことは禁止されている。 従って、③-.37はルール違反である。 なお、整数の定義には、符号 数字列 とあるので、⑤-125は許されるし、さらに、数値は 整数 小数 と定義され、整数は 符号 数字列 と定義され ①-9.1も許される。 Ⅰ-2-5 ハミング距離 解答:⑤ ハミング距離に関する出題である。 (ア)1110001と0001110を重ね合わせて、一致しない箇所は7か所である。 (イ)(ア)の解答が決定したので、(イ)に入るのは 「➃1001010」か「⑤」1011010」 のどちらかである。 7桁のビット列は送信過程で高々1ビットしか通信の誤りが起こらないとの仮定である。受信ビット列「1001010」の頭4文字の情報ビット列「1001」を取り出し、許される4つの並びA~Dを表に示した。また、この候補となる送信ビットから付加ビットを創生した。 表の「送信ビット」+「付加ビット」と候補となる➃および⑤の受信ビット列のハミング距離を求めたところ、その候補として「1011011」(ハミング距離1)が有力な候補であることが分かった。従って答は⑤となる。  情報理論において、ハミング距離(ハミングきょり、英: Hamming distance)とは、等しい文字数を持つ二つの文字列の中で、対応する位置にある異なった文字の個数である。別の言い方をすれば、ハミング距離は、ある文字列を別の文字列に変形する際に必要な置換回数を計測したものである。(Wikipedia) Ⅰ-2-6 スタック ボーナス問題です 解答:② 後入れ先出しです。一番最後にスタックに入れたデータが一番最初に取り出されます。 PUSHI 1 1 PUSH 2 2 1 PUSH 3 3 2 1 PUSH 4 4 3 2 1 POP 3 2 1 4が取り出される POP 2 1 3が取り出される PUSH 5 5 2 1 POP 2 1 5が取り出される POP 1 2が取り出される 3群 解析に関するもの R01年 基礎科目問題 トップに戻る Ⅰ-3-1 偏微分 サービス問題です 過去にも似た問題が数回出題されています 解答:⑤ 素直に計算するのみです。 divV=∂Vx/∂x+∂Vy/∂y+∂Vz/∂z =∂sin(x+y+z)/∂x+∂cos(x+y+z)/∂y+∂z/∂z =cos(x+y+z)-sin(x+y+z)+1 =cos(2π)-sin(2π)+1 =1-0+1=2 Ⅰ-3-2 行列式 難しそうに見えますがサービス問題です 解答:⑤  Ⅰ-3-3 物体の落下運動方程式 サービス問題です 解答:① 等速運動は、dv/dt=0、従ってmg=kv、よってv=mg/k Ⅰ-3-4 ポアソン比 平成20年度Ⅰ-3-3に同じ 解答:④ 今、縦と横の長さがともにW0で長さ方向の長さがL0の直方体を考える。 長さ方向に引っ張ったとき、長さ方向ののびがΔL、縦と横方向の縮みがそれぞれΔWとする。この直方体の引張り力を加える前後での体積をゼロと置き、 体積変化ΔV=(W0-ΔW)2×(L0+ΔL)-W02×L0=0 Δが2回掛け算となる項は小さいので、これを無視して変形すると ΔW/W0=1/2×ΔL/L0 ポアソン比νの定義が ΔW/W0=ν×ΔL/L0 であるから、ν=1/2となる。 (参考)
Ⅰ-3-5 ひずみエネルギー 解答:④ ひずみエネルギー 短軸膨張の場合 からの借用です。 http://www.mech-kait.net/student/misawa/zairiki-shiryo/strain-energy.pdf
Ⅰ-3-6 剛体振り子の周期 解答:③ まずはウォーミングアップ。Θ=a×sin(ωt+c)として解くと、問題文に与えられている角振動数ωが得られます。 振り子の周期Tは、T=2π/ω=2π(2I/(Mgl))0.5となります。 問題は、この系における慣性モーメントIの大きさです。 慣性モーメントIは 剛体振り子の運動方程式を算出する にその求め方が記載されています。   この慣性モーメントIpを上の周期Tに代入すると、答えとして③が得られます。 この問題は、慣性モーメントが導出できるかを問う問題です。 さらに詳細はこちらのブログを参照してください。 4群 材料・化学・バイオに関するもの群 R01年 基礎科目問題 トップに戻る Ⅰ-4-1 ハロゲンとハロゲン化水素の性質 解答:➃ は表より、 (ア)誤 酸としての強さはHI>HBr>HCl>HF。逆である。 (イ)正 電気陰性度は数字が大きいほど大きい。正しい記載である。 (ウ)誤 ハロゲン化水素の沸点は高いものから、HF>HI>HBr>HClである。 (エ)正 問題文記載の通りであり、正しい。
Ⅰ-4-2 同位体 正解:⑤ 同位体(どういたい、英: isotope;アイソトープ)とは、同一原子番号を持つものの中性子数(質量数 A - 原子番号 Z)が異なる核種の関係をいう。(Wikipedia) (ア)誤 陽子の数と電子の数が同じであれば帯電していない原子である。陽子の数>電子の数であれば原子はプラスに帯電(カチオンという)。逆ならばマイナスに帯電(アニオンという)している。同位体とは関係のない内容である。 (イ)誤 原子の化学的性質は陽子の数で決まり、中性子の数は関係しない。 (ウ)正 記載の通りである。たとえば、最近問題になっているトリチウムは水素の一種であるが、陽子1個と中性子2個からなる核を持っている。中性子が1個ならば重水素、そして陽子の実ならば単に水素である。 (エ)正 記載通りである。 放射性同位体(密封線源)から出る放射線は、放射線療法によるがんなどの治療、突然変異誘発による作物育種、非破壊検査、火災報知機などに応用される。 (Wikipedia、放射性同位体) 放射性炭素年代測定は、自然の生物圏内において放射性同位体である炭素14 (14C) の存在比率が1兆個につき1個のレベルと一定であることを基にした年代測定方法である。対象は動植物の遺骸に限られ、無機物及び金属では測定が出来ない。(Wikipedia) (オ)正 記載通りである。 放射性同位体の崩壊は核種の変位法則に従い、アルファ崩壊により原子番号と質量数の異なる核種へ、またはベータ崩壊により同質量数で原子番号の異なる核種へと放射性崩壊を起こす。ガンマ崩壊では質量数も原子番号も不変である。一部の超ウラン元素等は自重に耐えられずに自発的に核分裂を起こして崩壊し、中性子を出すこともある。(Wikipedia、放射性同位体) Ⅰ-4-3 原子数比率を求める ボーナス問題である 平成27年度Ⅰ-4-3に同じ問題がある 正解:④ 重量比で与えられているものを原子数の比に換算する。 Al:Cu=95.5/27:4.5/63.5=98.0:1.96 Ⅰ-4-4 知識を試す問題 解答:③ ①誤 炭酸ナトリウム(たんさんナトリウム、sodium carbonate、別名:炭酸ソーダ)は組成式 Na2CO3、式量106のアルカリ金属炭酸塩である。水酸化ナトリウムとその半分の物質量の二酸化炭素を反応させるか、炭酸水素ナトリウムを熱すると得られる。 ハーバー・ボッシュ法は窒素と水素よりアンモニアを製造する方法である。 ②誤 黄リン(P4)は四面体形の分子からなり、比重が1.82、融点が44.1 ℃、沸点が280℃の、常温常圧で白色ロウ状の固体である。発火点は約60℃で些細なことで自然発火するため、水中で保存する。空気中で室温でも徐々に酸化され、熱および青白い光を発する。現在、燐光は別の発光現象の意味で用いられているが、その語源でもある。ベンゼン、二硫化炭素(CS2)などの有機溶媒によく溶ける。強い毒性を持ち、ニンニクのような臭いがある。日光にあたると赤リンに変化する。(Wikipedia) ③正 記載の通りである。 ➃誤 ダイヤモンドのことをいっている。グラファイト(黒鉛)の性質も示す。  ⑤誤 鉛蓄電池の電極における化学反応は下記で示され、PbとPbO2におけるPbの酸化数の差を利用した電池である。(Wikipedia)  一般的には、珪砂(SiO2)、カリウム、ソーダ灰というガラスの主成分に、酸化鉛(PbO)を添加して形成される鉛ガラスの一種を指す。 ガラスの製造時に酸化鉛等を添加することでガラスの溶解温度が低く抑えられ成形もソーダガラスに比べて容易になること、また透明度と屈折率が高まり水晶(クリスタル)のように輝く透明なガラスになることから、通称として「クリスタル」と呼ばれる。(Wikipedia、クリスタル・ガラス) Ⅰ-4-5 DNA二重らせん 頻出問題であり得点源である ボーナス問題 解答:④
Ⅰ-4-6 タンパク質 頻出問題であり得点源である ボーナス問題 解答:③ 詳細な解説は省略する。 タンパク質を構成するアミノ酸20種はWikipediaを参照のこと。ここには各アミノ酸ごとの等電点も記されています。アミノ酸がペプチド結合してタンパク質となる。高いpHとはアルカリ性(塩基性)のことで、タンパク質のカルボキシル基(-COOH)の水素を奪いマイナスイオン(-COO-)とし、負に帯電する。逆に低いpH(酸性)ではタンパク質を構成するアミノ基(-NH2、-NH-)などにプロトン(H+)が付加して(-NH3+、-NH2+-)となり、タンパク質は正に帯電する。 アミノ酸はアミノ基とカルボキシル基の両方を持っているので等電点がある代表的な化合物であるが、カルボキシル基を複数もつ酸性アミノ酸(アスパラギン酸及びグルタミン酸)は一般に等電点が低く、アミノ基を複数もつ塩基性アミノ酸(アルギニン、ヒスチジン及びリシン)は一般に等電点が高い。その他の中性アミノ酸の等電点はアミノ基の酸解離定数(pKa) とカルボキシル基の酸解離定数を足して2で割ると容易に算出できる。(Wikipedia,等電点) 5群 環境・エネルギー・技術に関するもの R01年 基礎科目問題 トップに戻る Ⅰ-5-1 大気汚染 ボーナス問題です 解答:③ 特に解説の必要はないと思います。若い受験者にわかりにくいのは光化学オキシダントでしょう。 光化学オキシダント(こうかがくオキシダント、英語: photochemical oxidant)は、窒素酸化物と炭化水素とが光化学反応を起こし生じる、オゾンやパーオキシアシルナイトレートなどの酸化性物質(オキシダント)の総称である。オキシダント (oxidant) は酸化剤 (oxidizing agent) のこと。強力な酸化作用を持ち健康被害を引き起こす大気汚染物質であり、光化学スモッグの原因となる。(Wikipedia) Ⅰ-5-2 環境保全・環境管理 平成29年度Ⅰ-5-2 パリ協定です 解答:② 温室効果ガスの排出削減に向けての本対策は、「適応策」ではなく、「緩和策」ということです。パリ協定の第4条(緩和・排出のための取組)となっています。 Ⅰ-5-3 長期エネルギー需給見通し 平成28年度Ⅰ-5-4です 解答:③ 石油火力発電の比率は知っていなければならない問題です。経済産業省の「長期エネルギー需給見通し」を確認ください。 図は平成28年度Ⅰ-5-4の解答より。   Ⅰ-5-4 二酸化炭素発生量 ボーナス問題である 解答:④ 計算式のみ記します。 (5044×24+7831×19+4696×14)×44/12×103/106 = 1230Mt-CO2 順に、石炭、石油、天然ガス・都市ガス。C=12(原子量)、CO2=44(分子量) Ⅰ-5-5 科学史 解答:② ① 原子核分裂の発見(1938年) 原子力発電の開始(1951年) ② ウイルスの発見(19世紀~20世紀) 種痘(1796年) ルイ・パスツールとエドワード・ジェンナーはウイルスの感染を防ぐ最初のワクチンを開発したが、彼らはウイルスの存在を認識してはいなかった。(Wikipedia) ③ 望遠鏡の発明(1590年) 土星の輪の確認(1610年) ➃ 量子力学の誕生(1926年) トランジスターの発明(1947年) ⑤ 電磁波の存在確認(1888年) レーダーの開発(1904年) 1887年、ドイツの物理学者であるハインリヒ・ヘルツが電磁波の人工的な発生と検出に関する実験を行った。電磁波の存在はイギリスの物理学者であるジェームズ・クラーク・マクスウェルによって理論的に予言されていたが、ヘルツの実験によってはじめて立証された。 1904年、ドイツの発明家クリスティアン・ヒュルスマイヤー(Christian Hülsmeyer)はドイツとオランダで電磁波の反射で船を検出して衝突を避ける実演を行った。 Ⅰ-5-6 特許法と知的財産基本法 解答:⑤ 知的財産基本法に次のように書かれている。、 (国の責務) 第五条 国は、前二条に規定する知的財産の創造、保護及び活用に関する基本理念(以下「基本理念」という。)にのっとり、知的財産の創造、保護及び活用に関する施策を策定し、及び実施する責務を有する。 平成30年度の出題より、本年度の出題に関係ありそうな部分を以下に示しておきます。 R01年 基礎科目問題 トップに戻る H30年 基礎科目問題 Ⅰ-1-4 生産数量最適化 本年度のⅠ-1-1(イ)に関連 解答:② 文意より、次の表を作成した。赤枠で囲った部分が生産可能な製品1および製品2の生産量(各1時間当たり1kg)およびその生産に必要な原料AおよびBの量である。 販売で得られる利益は、製品1が300万円/kg、製品2が200万円/kgであるので、赤枠で囲った部分の利益合計は、 製品1 3 900万円 4 1200万円 5 1500万円 製品2 4 800万円 3 600万円 2 400万円 合計 1700万円 1800万円 1900万円 となり、答えは1900万円である。 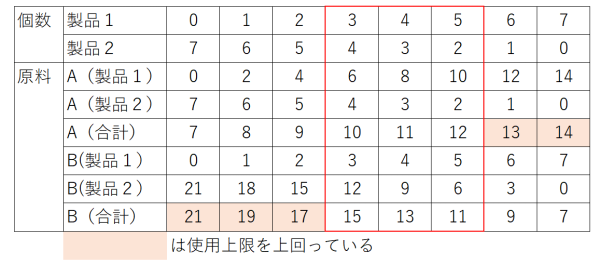 (別解) グラフを利用してこの問題を解くこともできる。製品1の生産量をx(kg)、製品2の生産量をy(kg)とすると、 x + y = 7 式1 2x + y ≦ 12 式2 x + 3y ≦ 15 式3 ゼロ点とx軸、y軸および式1の直線で囲まれる範囲が生産可能領域となり、式2と式3の交点、x=5、y=2はその領域に含まれる。 その点が最大利益を与える点であり、その利益額は、 利益額=300x+200y=1900万円 と計算される。作図は試みてください。 関連問題はH28年1-1-5 Ⅰ-2-5 2分木と後置記法 本年度のⅠ-2-2に関連 解答:① 問題文で例示されている図 数式を図に落とし、示された番号順に記号を並べていくと、数式が後置記法に変換される。 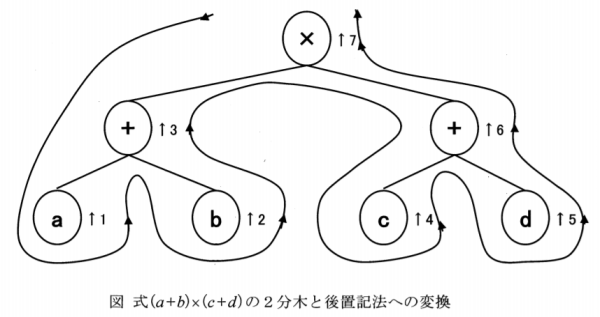 問題で後置記法への変換が求められている中間記法式は a×b+c÷d。この式の記号を図に当てはめ、例示図と同じに読んでいくと、ab×cd÷+ となる。 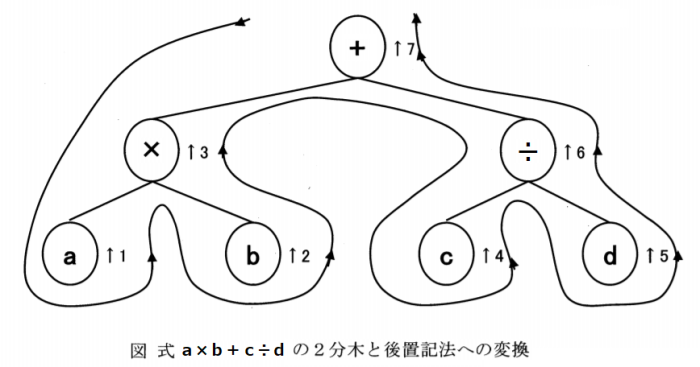 Ⅰ-3-2 偏微分 本年度のⅠ-3-1に関連 解答:④ u=-x2+2xy、v=2xy-y2 をそれぞれ与えられた条件で偏微分氏、得られた数式にx=1、y=2を代入する問題である。 div u = -2x+2y+2x-2y = 0 rot v = 2y-2x = 2 過去に類似の問題としてH27年Ⅰ-3-2がある。 Ⅰ-3-3 逆行列 本年度のⅠ-3-2に多少関連 解答:② 行列Aと逆行列A-1の掛け算をすると、単位行列が得られます。下図は掛け算の方法を示しています。 行列の掛け算 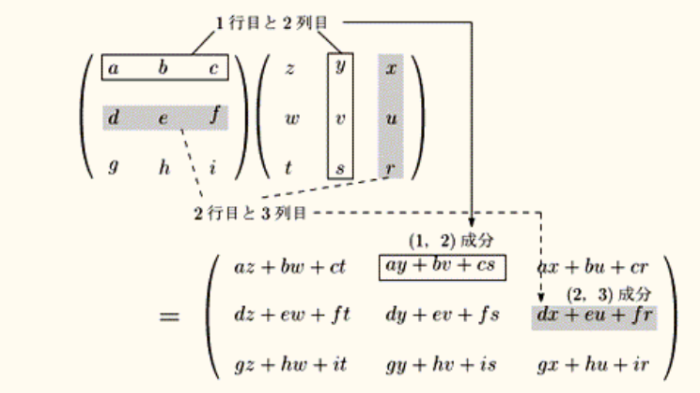 http://naop.jp/text/c/gyouretu3.html 単位行列 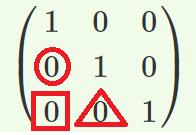 まず、掛け算の結果、〇で囲んだ部分がどうなるかを実際に計算してみました。この値が0でなければ解答候補から外れます。 ①a+a=2a、②-a+a=0、③1-a+a=1、④-a+a=0、⑤a+a=2a 解答の候補として、②と④が残りました。 次いで、②と➃について、□で囲んだ部分の値を計算しました。 ②ac-b-ac+b=0、④ac+b-ac+b=2b 従って、消去法で②が答えとして残ります。他の部分、例えば△などについての計算はしていません。 過去問 H25年Ⅰ-3-4に逆行列の問題がありました。 Ⅰ-3-6 ヤング率と材料の伸び 本年度のⅠ-3-4に関連 解答:③ 過去にも関連する多くの問題が出題されています。 σ=F/S=E・ΔL/Lの式と、 1N=1kg・m/s2、および1Pa=1N/m2=1kg/(m・s2) がわかっていれば解ける、簡単な問題群です。 計算間違いをしなければ正答に行きつけます。 H22年 Ⅰ-3-5 本年度のⅠ-3-4に関連  正答: ② (解答) ΔL=FL/(SE) =1000(kg・m・s2)×1m/(100×10-6(m2)×100×109(kg・(m・s2)) =10-4m =0.1mm Ⅰ-5-3 石油情勢 本年度のⅠ-5-3に関連 解答:③
|



