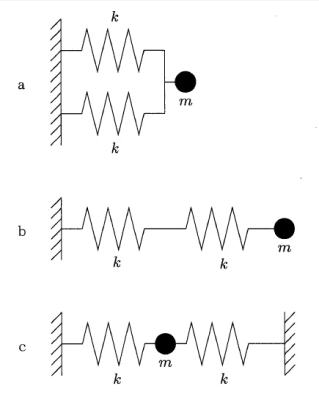
Ｃ０５　　バネの固有振動数 この問題の努力目標 　　理解する　イメージする 技術士試験の問題からは必要最小限の引用にとどめる。（問題）が記されている部分はその引用である。 問題および解答は日本技術士会のホームページより必要に応じて入手してください。 　　技術士第一次試験の問題　　　　　　 バネの固有振動数 問題番号が赤字のものは、ボーナス問題 Ｈ２６年　Ⅰ－３－５　　　Ｈ２４年　Ⅰ－３－２ 同じ問題 Ｈ２６年　Ⅰ－３－５　と　Ｈ２４年　Ⅰ－３－２ バネのエネルギー Ｈ２２年　Ⅰ－３－４　　　Ｈ１６年　１－３－１ バネの固有振動数 Ｈ２６年　Ⅰ－３－５ 正答：　② （解答） バネが強いほど、そして重りが軽いほど、バネは速く振動する。これは日常の経験からわかる。 図ａと図ｃは違うように見えるが、振動に関しては同じである。 重りの位置がΔｘ移動すると、バネが１本の場合と比較して２倍の力がかかる。一方、図ｂではバネが２本直列につながった結果、重りの位置がΔｘ移動した場合、バネ１本あたりでは０．５Δｘの移動となり、バネが１本の場合と比べてかかる力は０．５倍となる。固有振動数は１／（２π）×√（ｋ／ｍ）で与えられ、①（１／（２π）×√（２ｋ／ｍ）、②１／（２π）×√（ｋ／（２ｍ））、③１／（２π）×√（２ｋ／ｍ）となる。 ａ　と　ｃ　のバネの位置は違っているように見えるが、振動数に関してはその作用が同じであることに思い至れば、簡単な問題である。 バネのエネルギー H２２年　Ⅰ－３－４　 正答：　②　 （解答） バネの基本公式は、 　　　　Ｆ＝－ｋｘ バネ定数２ｋのバネを直列につないでいるから、合成バネ定数は、　１／（１／（２ｋ）＋１／（２ｋ））＝ｋ （強いばねでも、直列につなぐとそのバネ定数は小さくなります。小さな力でも伸ばせるようになります） 従って、このバネの伸びと力の関係を表す式は、 　　　　Ｆ＝－ｋｘ エネルギーは力×距離　　バネを釣合の状態から　ｘ　伸ばすときを考える。 　　　　Ｅ＝∫Ｆｄｘ＝－ｋ∫ｘｄｘ＝[－ｋｘ２／２]（ｘ＝０ ｔｏ ｋ）＝－ｋｘ２／２ このバネの、重荷Ｐと釣り合う距離ｘは、 　　　　Ｐ＝－ｋｘ　より　ｘ＝－Ｐ／ｋ 従って、　Ｅ＝－ｋｘ２／２＝－ｋ（－ｐ／ｋ）２／２＝－Ｐ２／（２ｋ） Ｈ１６年　１－３－１ 正答：　④ （解答） 間違っているのは④です。 ①　全ポテンシャルエネルギー＝内部ポテンシャルエネルギー＋外部のポテンシャルエネルギーです。内部ポテンシャルエネルギーを失うとその失った分だけ外部のポテンシャルエネルギーが増える、あるいはその逆となりますが、全ポテンシャルエネルギーは一定という構図です。バネが伸びた場合、そのバネの内部に蓄えられる内部エネルギーはｋｕ２／２、一方、重りは高さがｕ下がり位置のエネルギーを失いますから－ｍｇｕ。この合計、ｋｕ２／２－ｍｇｕが一定となります。 ②　バネの伸びに必要な力と重りが重力より受ける力の釣合の式です。 ③　①の式、ｋｕ２／２－ｍｇｕをｕで微分すると、ｋｕ－ｍｇ、これをゼロと置くとｋｕ＝ｍｇとなり②と同じ話となる。 ④　全ポテンシャルエネルギーは一定。位置のエネルギーと運動のエネルギーが移り変わっていくが、その合計は一定である。この④で言っていることは、①で言っていたことと違っていることが分かれば、①か④のどちらかが誤りであることがわかる。 ⑤　有限要素法の基本は、静止している系のメッシュ切りを行うことにあるが、動いている系ではこのメッシュが切れない。 　　　　　　　　　　　　　　　　問題一覧表へ戻る