| C06 有限要素法 基本 努力目標 理解し覚える 技術士試験の問題からは必要最小限の引用にとどめる。(問題)が記されている部分はその引用である。 問題および解答は日本技術士会のホームページより必要に応じて入手してください。 技術士第一次試験の問題 問題番号が赤字のものは、ボーナス問題 有限要素法 数値解析精度 H27年 1-3-3 H26年 Ⅰ-3-2 H18年 Ⅰ-3-1 H17年 Ⅰ-3-2 同じ問題 H27年 Ⅰ-3-3 と H17年 Ⅰ-3-2 有限要素法記述に関する正誤 H24年 Ⅰ-3-1 H23年 Ⅰ-3-1 H19年 Ⅰ-3-2 H18年 Ⅰ-3-4 同じ問題 H24年 Ⅰ-3-1 と H19年 Ⅰ-3-2 有限要素法の数値解析精度 H27年 Ⅰ-3-3 正答: ① (解答) ① 下に示したWikipediaからの引用の通り。 ② 曲線を直線で近似する段階で、すでに誤差が入り込んでいる。 ③ 格子幅が広いと、通常は誤差が大きくなる。 ④ 要素分割を小さくすると誤差は小さくなる。 ⑤ アルゴリズムにより計算精度を変えることができる。 (参考) 誤差(Wikipedia) 実例を示し、解説されています(詳細はWikipediaのページへ)。誤差の原因に関する部分を抜粋しました。 計算誤差の種類丸め誤差数値を、どこかの桁で端数処理(切り上げ・切り捨て・四捨五入・五捨六入・丸めなど)をしたときに生じる誤差。 打ち切り誤差計算処理を続ければ精度がよくなるにもかかわらず、途中で計算を止めること(打ち切り)によって生じる誤差。 情報落ちコンピュータでの計算のときのように有効桁数が限られている条件下で、絶対値の大きい数と絶対値の小さい数を加減算したとき、絶対値の小さい数が無視されてしまう現象。 桁落ち桁落ち(けたおち)とは、値がほぼ等しく丸め誤差を持つ数値同士の減算を行った場合、有効数字が減少すること。絶対値がほぼ等しく符号が異なる数値どうしの加算の場合も同様。浮動小数点数では、上位の桁がゼロになると、正規化によってそれを詰め、以下の桁に"0" を強制的に挿入するので、下位の桁が信頼できないものになる。特別な場合には、演算式を変形することによって、桁落ちを避けることができる。 各数値形式に発生する誤差
○印は誤差が発生しうることを示す H26年 Ⅰ-3-2 正答: ③ 常識を問う問題です。 (解答) ① 要素分割を細かくすると精度が向上します。 ② 高次の分割を行うことで精度が向上します。下の(参考)をご覧ください。 ③ 収束判定条件を緩和することは、誤差の大きさを許容することになる。 ④ 曲率の小さな部分などは細かく要素分割する必要がある。 ⑤ 倍精度は単精度に対して扱える数値の有効桁数が多い。 (参考) 有限要素法(機械設計エンジニアの基礎知識)よりの引用です。 ここに引用したのはその一部です。詳しく、しかも分かり易く解説されています。 メッシュのタイプと計算精度メッシュには、以下のタイプが存在します。
メッシュのタイプによって、計算精度が異なります。 計算精度をさらに良くするためには、メッシュの次数を上げます。 「メッシュの次数を上げる」 とは、接点間に中間節点を入れるということです。先ほどの要素が 「1次要素」 であるのに対して、中間節点を入れた要素を 「2次要素」 といいます。
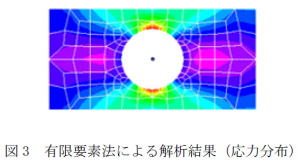
有限要素法の記述に関する正誤 以下の一連の問題では誤っているものを選ぶ。 従って、5つの設問の内の4つは正解である。 誤っているものの一部は問題文を正解に戻して記述した。 こういうものだと、ひたすら記憶する。 H24年 Ⅰ-3-1 正答: ① (解答) 「粗い要素分割で解析した場合には常に変形は小さくなり応力は高めになるので、応力評価に関しては安全側である。」は誤り。 応力評価に関しては不安全側である。下の(参考)を見てください。 要素分割の影響を見るため、できれば複数の要素分割によって解析を行い、結果を比較するのが望ましい。 ある荷重に対して有効性が確認された要素分割でも、他の荷重に対しては有効とは限らない。 応力の変化が小さい部分に対しては、応力自体の大小にかかわらず要素分割の影響は小さい。 応力の変化が大きい部分に対しては、要素分割を細かくするべきである。 (参考) 超重要! メッシュサイズと8つの質問(設計者CAEを始める前にシッカリ学ぶ有限要素法)より抜粋 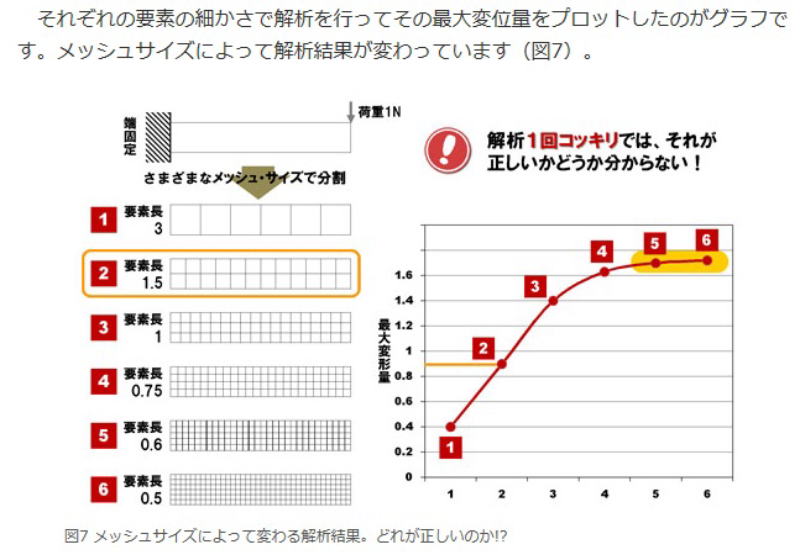 H23年 Ⅰ-3-1 正答: ② (解答) 応力値は、隣接要素との共通辺を横切るとき不連続となる。 |