Ｃ１８　　定積分近似式 努力目標 　　式の意味を理解する 技術士試験の問題からは必要最小限の引用にとどめる。（問題）が記されている部分はその引用である。 問題および解答は日本技術士会のホームページより必要に応じて入手してください。 　　技術士第一次試験の問題　　　　　 問題番号が赤字のものは、ボーナス問題 H２８年　Ⅰ－３－１　　　Ｈ１８年　Ⅰ－３－２ H２８年　Ⅰ－３－１ 正答：　③ （解答） この問題の意味をイメージでとらえる。 問題の意味は、ｘ軸とｆ（ｘ）で囲まれた、Ｘ＝－１からＸ＝１までの面積を積分で求めるというものである。 ①　ｆ（－１）とｆ（１）の中間点ｆ（０）を妥協高さとして、長方形の面積を求めている。 ②　ｆ（－１）とｆ（１）を頂点とする台形の面積を求めている。 ③　？？？？ ④　（①＋②）／２である。 ⑤　①×１／３＋④×２／３である。 以上、説明を加えたが、一番端的なのは、それぞれのｆ（ｘ）の係数を足した数字が、③のみ２とならないことである。 ①２　②１＋１＝２　③１／４＋１＋１／４＝３／２　④１／２＋１＋１／２＝２　⑤１／3＋４／３＋１／３＝２ Ｈ１８年　Ⅰ－３－２ 正答：　④　 （解答） 適当な図を作成し、それぞれの意味を考えてみる。 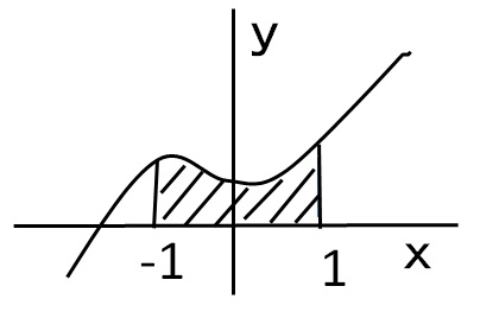∫ｆ（ｘ）ｄｘ（ｘ＝－１ ｔｏ １）はｘ＝－１～１区間におけるｘ軸と曲線に挟まれた面積である。 式①②③⑤はなんとか近似面積を出そうと努力していが、④の意味は不明である。 ①　高さｆ（０）×幅２ ②　高さｆ（１）×幅１＋高さｆ（－１）×幅１ ③　（ｆ（１）とｆ（０）の平均）×幅１＋（ｆ（０）とｆ（－１）の平均）×幅１ ⑤　①×１／２＋③×２／３ ポイントは式の係数を合計すると２となること（ｘが－１～１の範囲、幅は２）。例えば⑤は１／２＋４／３＋１／３＝２、これに対して④は１／４＋１＋１／４＝１．５。 　　　　　　　　　　　　　　　　問題一覧表へ戻る