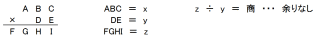１〜９の整数すべてを用いる掛け算

２桁の整数と３桁の整数を掛け合わせて４桁の整数としたとき、
１から９までの全ての数字がすべて現れる場合はあるか？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２０１５．２．６　畑　啓之

この問題は世の中に今まであったかどうかはわからないが、表題の可能性はあるか？　あれば幾通りのケースが存在するか？　に興味を持ったので、その答えを導く試みをすることにした。この問題を図示すれば次のとおりであり、出てくる数字の桁数は２桁、３桁、そして４桁であるので、合計すると９桁となる。従って、運がよければ、A〜Iのアルファベット記号の場所にそれぞれ１〜９の数字が１回ずつ入る。



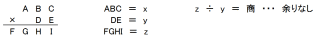
この問題、少し睨んでいたくらいでは答えが存在するかどうかさえもわからない。

そこで、コンピュータプログラムを組み、その答えの有無と、もし答えがあった場合にはその組み合わせについて確認することにした。これ以外に良い方法を思いつかなかったからである。


まず、組み上げたコンピュータプログラムは次のとおりである。プログラムとしては単純な構成であると思うが、その説明を下で行っている。



Excel-VBA　プログラム


Sub 掛け算()

Dim x As Integer, y As Integer, z As Integer, i As Integer
Dim j As Integer, k As Integer, n As Integer, ans As Integer,
Dim kazu(9) As Integer

n = 1
For j = 1234 To 9876
　　For i = 12 To 98
　　If j Mod i = 0 And j / i > 100 Then Cells(20 + n, 2) = j \ i: Cells(20 + n, 3) = i: Cells(20 + n, 4) = j: n = n + 1
　　Next i
Next j

For i = 1 To n
　　x = Cells(i + 20, 2): y = Cells(i + 20, 3): z = Cells(i + 20, 4)
　　Cells(i + 20, 6) = x \ 100: Cells(i + 20, 7) = x \ 10 - Cells(i + 20, 6) * 10: Cells(i + 20, 8) = x - Cells(i + 20, 6) * 100 - Cells(i + 20, 7) * 10
　　Cells(i + 20, 9) = y \ 10: Cells(i + 20, 10) = y - Cells(i + 20, 9) * 10
　　Cells(i + 20, 11) = z \ 1000: Cells(i + 20, 12) = z \ 100 - Cells(i + 20, 11) * 10: Cells(i + 20, 13) = z \ 10 - Cells(i + 20, 11) * 100 - Cells(i + 20, 12) * 10: 　　Cells(i + 20, 14) = z - Cells(i + 20, 11) * 1000 - Cells(i + 20, 12) * 100 - Cells(i + 20, 13) * 10
Next i


For k = 1 To n

For j = 1 To 9: kazu(j) = 0: Next j

For j = 6 To 14
　　x = Cells(k, j)
　　If x = 0 Then GoTo skip
　　kazu(x) = kazu(x) + 1
　　If kazu(x) >= 2 Then GoTo skip
Next j

For j = 2 To 14: Cells(k, j).Interior.ColorIndex = 6: Next j

For j = 2 To 14: Cells(8 + ans, j) = Cells(k, j): Next j: ans = ans + 1

skip:

Next k


End Sub

プログラムの説明

このプログラムの構成を説明する前に、まずプログラム中に出てくる数値x、y、zとは何かを示しておく必要がある。数値xとは上図の数値ABC、yとは同じくDE、そして積zは同じくFGHIを表している。

プログラムの基本的な考え方は、次の３ステップよりなる。
１．積zを数値yで割り算した時、その答えがxとなるが、この時に余りがゼロであれば、x×y＝zの整数計算が成立していることになる。
　　まずはz÷y＝商・・・・余りで余りがゼロのケースを探す。
２．x、y、zを構成する９つの整数、A〜Iを書き出す。
３．書き出した９つの整数に１〜９の整数がそれぞれ１回ずつ現れることを確認する。この試験にパスしたものが求める組み合わせである。

この考え方に従って次のプログラムを組んだ。


Excel-VBA　プログラム


Sub 掛け算()
　　　　　　プログラム名を示している。


※※※※※　ステップ　１　※※※※※

Dim x As Integer, y As Integer, z As Integer, i As Integer
Dim j As Integer, k As Integer, n As Integer, ans As Integer,
Dim kazu(9) As Integer
　　　　　　下のプログラムで出てくる変数名の種類を定義する。Integerはここに示した変数が全て整数であることを示している。
n = 1
For j = 1234 To 9876
　　　　　　これはz、すなわち４桁の積が１２３４と９８７６の間にあり、その全ての整数を順番にz÷yの計算式に当てはめることを意味している。
　　For i = 12 To 98
　　　　　　これはy、すなわち２桁の整数が１２と９８の間にあり、その全ての整数を順番にz÷yの計算式に当てはめることを意味している。
　　If j Mod i = 0 And j / i > 100 Then Cells(20 + n, 2) = j \ i: Cells(20 + n, 3) = i: Cells(20 + n, 4) = j: n = n + 1
　　　　　　z÷yの計算結果に余りがない場合には、その数値x、y、zを行番号２１番目から順番に書き出していく。
　　　　　　j Mod ｉ は、j　を　ｉ　で割った場合の余りを与え、これがゼロであることは余りがないということである。
　　　　　　また、yは３桁の数値であるから、j/i>100としている。9876/12=823と３桁であるが、1234/98=12と２桁になってしまうため。
　　Next i
Next j


※※※※※　ステップ　２　※※※※※

For i = 1 To n
　　　　　　ステップ１でヒットしたすべての組み合わせについて、
　　x = Cells(i + 20, 2): y = Cells(i + 20, 3): z = Cells(i + 20, 4)
　　　　　　ステップ１で求めたx、y、zを呼び出す。
　　Cells(i + 20, 6) = x \ 100: Cells(i + 20, 7) = x \ 10 - Cells(i + 20, 6) * 10: Cells(i + 20, 8) = x - Cells(i + 20, 6) * 100 - Cells(i + 20, 7) * 10
　　　　　　xよりA、B、Cを切り出す。x\100はxを100で割った時の商、すなわち３桁目の数値Aを示す。同じくBとCを求める。
　　Cells(i + 20, 9) = y \ 10: Cells(i + 20, 10) = y - Cells(i + 20, 9) * 10
　　　　　　yよりDとEを切り出す。
　　Cells(i + 20, 11) = z \ 1000: Cells(i + 20, 12) = z \ 100 - Cells(i + 20, 11) * 10: Cells(i + 20, 13) = z \ 10 - Cells(i + 20, 11) * 100 - Cells(i + 20, 12) * 10: 　 Cells(i + 20, 14) = z - Cells(i + 20, 11) * 1000 - Cells(i + 20, 12) * 100 - Cells(i + 20, 13) * 10
　　　　　　zよりF、G、HとIを切り出す。
Next i

※　各数字からのＡ〜Ｉの切り出しにＭｉｄを用いるとこの部分は非常に簡単になる。


※※※※※　ステップ　３　※※※※※

For k = 1 To n
　　　　　　ステップ１でヒットしたすべての組み合わせについて、
For j = 1 To 9: kazu(j) = 0: Next j
　　　　　　ステップ２で分解した数値の出現回数を記録するカウンターを整える（初期値をゼロとする）。
　　　　　　例えばkazu(1)は数値１が１度出てくるとそのカウンターは１となり、もう一度出てくるとカウンターを２とする。
　　　　　　kazu(1)には
For j = 6 To 14
　　x = Cells(k, j)
　　If x = 0 Then GoTo skip
　　kazu(x) = kazu(x) + 1
　　If kazu(x) >= 2 Then GoTo skip
　　　　　　各数値は１度ずつ出てくることが条件なので、カウンターが２となるとこの条件に反することとなる。
　　　　　　この場合には、このFor〜Nextルーチンから抜け出して、下のskipに飛ぶ。
Next j

For j = 2 To 14: Cells(k, j).Interior.ColorIndex = 6: Next j
　　　　　　A〜Iに１〜９が１回ずつ入る組み合わせに黄色の目印を付ける。

For j = 2 To 14: Cells(8 + ans, j) = Cells(k, j): Next j: ans = ans + 1
　　　　　　同時に、このヒットした組み合わせを行番号８から順番に書き出す。

skip:

Next k


End Sub
　　　　　　プログラムの終了

得られた結果

次の７つの組み合わせが条件を満足することが確かめられた。




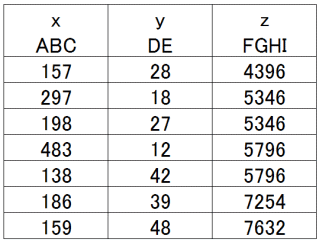
ここで得られた積ｚはすべて偶数となった。１〜９には奇数が５個、偶数が４個含まれる。ｘとｙの両方あるいは一方が偶数ならば積ｚは偶数、共に奇数ならば積ｚは奇数となる。すなわち、5/9×5/9＝25/81の確率で積ｚに奇数があってもよいことになりそうであるが、実際にはそうはならなかった。（組み合わせの数は表に示した通り７個であるので、７×25/81＝２．２となる。）





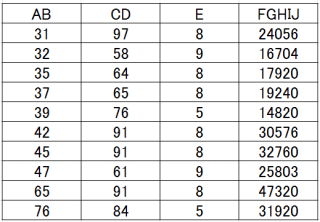
同じく、３桁×２桁＝５桁の計算で、０から９までのすべての数字が現れる組み合わせはつぎの９通り。得られた積は偶数が８個、奇数が１個となりました。







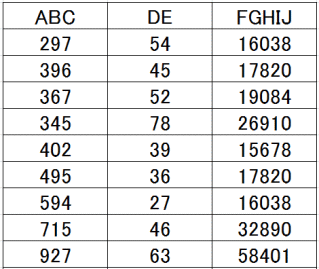
AB×CD×E=FGHIJでは

MIDを使う。
０〜９の個数の判定に工夫を加える。


Sub kakezan2215()

Dim a As Long, b As Long, c As Long, d As Long
Dim sa As String, sb As String, sc As String, sd As String
Dim z(10) As String

For a = 12 To 98
For b = 12 To 98
For c = 1 To 9
d = a * b * c

sa = CStr(a)
sb = CStr(b)
sc = CStr(c)
sd = CStr(d)

If Len(sa) + Len(sb) + Len(sc) + Len(sd) <> 10 Then GoTo skip

z(1) = Mid(sa, 1, 1): z(2) = Mid(sa, 2, 1)
z(3) = Mid(sb, 1, 1): z(4) = Mid(sb, 2, 1)
z(5) = sc
z(6) = Mid(sd, 1, 1): z(7) = Mid(sd, 2, 1): z(8) = Mid(sd, 3, 1): z(9) = Mid(sd, 4, 1): z(10) = Mid(sd, 5, 1)

Total = 0: kake = 1: di = 0: tri = 0: tetra = 0
For i = 1 To 10
Total = Total + z(i)
di = di + z(i) ^ 2
tri = tri + z(i) ^ 3
tetra = tetra + z(i) ^ 4
kake = kake * z(i)

Next i

If Total = 45 And di = 285 And tri = 2025 And tetra = 15333 And kake = 0 Then X = 1 Else GoTo skip
Cells(1 + ncount, 1) = a: Cells(1 + ncount, 2) = b: Cells(1 + ncount, 3) = c: Cells(1 + ncount, 4) = d
For i = 1 To 10: Cells(1 + ncount, 4 + i) = z(i): Next i: ncount = ncount + 1

skip:

Next c
Next b
Next a

End Sub





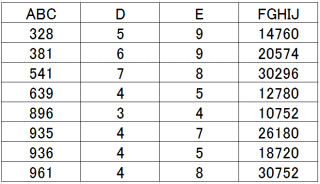
同じく、

ABC×D×E=FGHIJ










付録です。

整数Xと整数Yがあり、両者の関係は

　　　　　√（X)　＝　Y

であり、かつXの桁数とYの桁数の合計が９桁のとき、この９桁に１から９までの数字がすべて現れるXとYはあるか？


　　　　　答えは　　　　　　X=３２１４８９　　　　　　Y=567

　　　　　　　　　　　　　　　　　　　　　ホームページ　アルケミストの小部屋　に戻る