上海（ゲーム）のクリア確率は？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２０１５年１月　畑啓之


上海（ゲーム）とはどのようなもの

上海（ゲーム）（Ｗｉｋｉｐｅｄｉａ）に本ゲームのルールが次のように記されている。

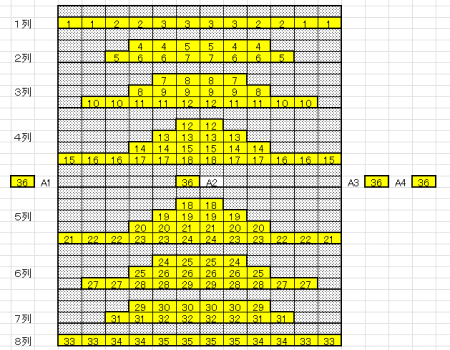
パソコンにはこの上海（ゲーム）（以降では単に上海と記す）が最初から入っているものが多い。次の図１と図２は、私のパソコンに入っている上海の初期配牌の一例である。図３は通常の麻雀牌の種類である。

図１　上海の配牌例１	図２　上海の配牌例２

上海で用いられる牌と、通常の麻雀で用いられる牌の関連を記したのが次の図だ。萬子（マンズ）は見やすいように「棒の本数」記号で記してある。筒子（ピンズ）、索子（ソウズ）はそのままの形で使われている。なお、索子の１は少しデザインが違っているが、上海に記されているのは竹に雀だ。竹と雀の組み合わせは掛け軸などにもよく描かれ、めでたいことの象徴だ。麻雀（Wikipedia)によると、「現在の中国語においては麻雀のことを一般に「麻将」（マージャン májiàng）という。「麻雀」（マーチュエ máquè）は中国語ではスズメを意味する。」となっており、この竹の１が麻雀の名の由来かもしれない。

風牌として「東南西北」の４種類がある。これらの牌は、私のパソコン中の上海では風を模した図案で描かれ、それぞれの色を変えるとともに左上隅に「E、S、W、N」の文字を配して識別してある。

麻雀の三元牌に相当するのが３色に色分けされた「龍」である。

萬子（９種類）、筒子（９種類）、索子（９種類）、四風牌（４種類）、三元牌（３種類）が通常の麻雀で用いられる牌３４種類である。上海ではさらに「植物」牌および「風景」牌の２種類を加え、合計で３６種類の牌としている。

図３　麻雀牌（Ｗｉｋｉｐｅｄｉａ）より	上海で用いられる牌	コンピュータ中での取り扱い
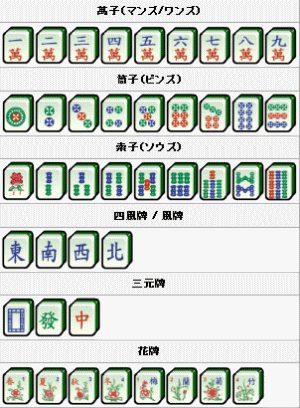	萬子牌　　　棒記号　９種類 筒子牌　　同じ表記　９種類 索子牌　　同じ表記　９種類 四風牌　風を図案化　４種類 三元牌　龍に図案化　３種類  花牌　植物を図案化　１種類 加えて 風景　風景を図案化　１種類 合計　３６種類 各牌４枚ずつで、合計１４４枚の牌を使用	それぞれの牌種に次の番号付を行って牌種を識別した。 萬子　　　　　　１　～　９ 筒子牌　　　　１０～１８ 索子牌　　　　１９～２７ 四風牌　　　　２８～３１ 　　ESWN　の順 龍牌　 　　　　３２～３４ 　　赤緑黒　の順 植物牌　　　　　　３５ 風景　　　　　　　３６ 合計　３６種類　×　４　＝　１４４枚

上海は絶対に解けるのか（クリアすることができるのか）

この疑問に答えるには、解けない例を探せば良い。思いつく例を３つ記した。

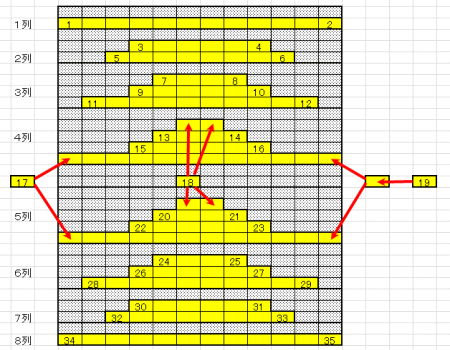
図４は絶対に解けない配牌である。配牌の時点で打つ手がない。説明は図の左に加えた。
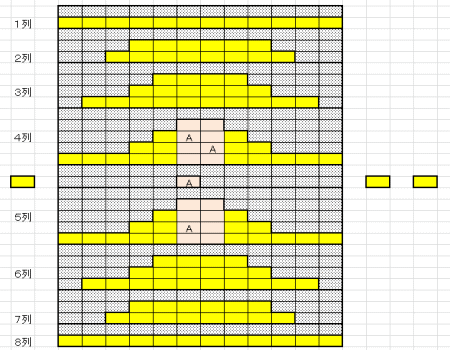
図５も頂上牌によりその下にある１６個の牌が影響を受ける。もしこの頂上牌と同種の残り３個の牌がこの１６個の牌に含まれていると解けなくなる。
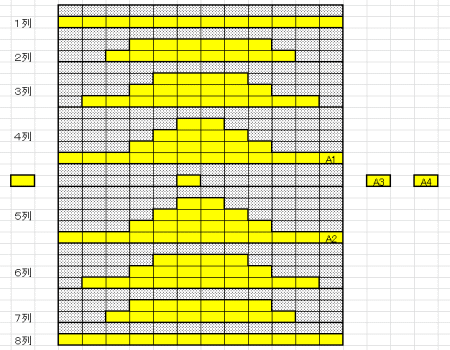
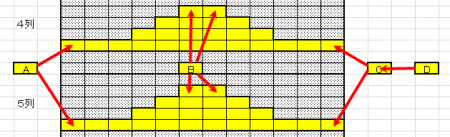
図６も同種の牌が右側に連なって存在している例だ。４列目、５列目の牌が左側からなくなって、やっと残ったA3牌とA4牌を消すことができるが、クリアできる確率はほぼ不可能と思える程に極めて低い。

図４　解けない配牌（その１）	図４の構成 　図１より、上海は上から順に８列の山より成り立っていることがわかる。さらに上４列と下４列の間には、そのちょうど中心の頂上部に頂上牌がひとつ置かれる。図１でいえばこれは索１（竹１）に相当する。 　この構成を図で示したのが、左図・図４である。１～８列を並べ、各列の積み重ねの様子も表現している。そして、中央部分には頂上牌を、図の両端には中央部の２列を両端から押さえ込んでいる牌を表現した。図１でいえば、左側の牌が索７（竹７）、右側の２個の牌が筒９と索６（竹６）に相当する。 ゲームの原則 　上で紹介した上海（Ｗｉｋｉｐｅｄｉａ）のとおりである。取り除くことが可能で、一致する牌があれば２個同時に取り除くことができる。赤矢印を入れたものは、矢印の根元の牌が残っている限り取り除くことができない。 図４に組み合わせペアが生じない理由 　使用する牌の種類は３６種類である。取り除くことが可能な牌は配牌時点で３５箇所である。従って、取り除ける可能性のある牌の位置に図のように異なった牌３５個を配することは可能で、そうした場合一致する牌がなくなる。
全く組み合わせを作ることができない配牌

図５　解けない配牌（その２）	図６　解くのが難しい配牌（その３）
頂上配が取り除けない限りその下にある牌も取り除けない	A1とA2が取り除かれる確率は極めて低い

図７　必ず解けると期待を抱かせる組み合わせ	図８　必ず解ける組み合わせ
ここに示した組み合わせは、それぞれの列の両端を素直に合わせていけばクリアできそうに感じられる。しかしながら、クリアできる確率は２／３、すなわち６７％である。 　見ていただくとわかるように、中央部分の頂上牌、４列と５列を左右より押さえ込んでいる牌３個の全てが同じ種類となっている。この４個の牌を図に示しているようにA1、A2、A3、A4とする。この中でまず取り除くことができる牌はA1、A2、A4の３個である。 　取り除き可能な組み合わせとしては、A1-A2、A1-A4、そしてA2-A4となる。この中で、A1-A2の組み合わせでは、A3とA4が残ることになり、図６で示した解けない組み合わせとなってしまう。残りの２つのケース、A1-A4とA2-A4の組み合わせならゲームをクリアすることができる。従って、ゲームをクリアできる確率は２／３となる。	図６での欠陥を改良したのがここに示した牌の並びである。A2とA4の牌を、上の第４列の第４段目の牌と入れ替えた。 　こうすることで、先ほど問題点であったA3とA4位置の牌が同種類で取り残されることがなくなり、その結果、この配牌では１００％の確率でこのゲームをクリアすることができる。

実際の上海のクリア確率は２８％程度

パソコンで上海に挑戦すると、回数を増やして行ってもそのクリアできる確率は２７～２９％の間で僅かな変動があるだけだ。これは私に学習能力がなく、このゲームを絶対にクリアしてやろうとの気概もないことがその原因となっている可能性が強い。目に付いたマッチング牌（ペア牌）を単純に取り除いていけば、この成功確率の範囲に自然に落ち着いてしまうということのようである。

１１回挑戦すればそのうちの３回はクリアできるこのゲームは、それなりに達成感（成功体験）が味わえるということだろう。何度やっても失敗続き（ゲームオーバー）では早期にやる気が失せるであろうし、必ずクリアできるゲームでは面白みもない。その点、この３割弱の成功確率は、ゲーマーをつなぎとめておくにはちょうど良い確率である。

上海は必ずクリアできるのか？　おそらくは毎回新たに提供される配牌はクリアできるように作ってあるだろう。穿った見方をすれば、提供される配牌のパターンの数はそんなに多くはなく、ゲームごとに複数種類の牌がその種類ごとに単に交換されているだけの可能性もある。今仮に６つの並びがあって、AABBCC、AACCBB、BBAACC、BBCCAA、CCAABB、CCBBAAの６つの並びは異なっていいるように見えるが、その基本的な並びは、１１２２３３のパターンである。１、２、３に入る記号A,B,Cの順番が入れ替わっているに過ぎない。このようなことをされても、私たちにはそのことがわからない。

このように、パターンが同じで牌の配置のみが入れ替わっている場合、新しく提供されたゲームのクリアできる確率は以前のものとは同じであるが、ゲーマーの目からは全く異なったものに見える。品質（クリアできる確率）を一定に保とうとすれば、このようなパターンは同じであるが牌のみを入れ替える方法はきっと講じられていることと思う。

とは言っても、ゲームの中には難しいものもあれば簡単なものもあり、平均して３割弱のクリア率になるものと考えられる。しかし、悲しいかな、私たちゲーマーは、同じゲームを多数回（例えば１００回以上）繰り返してそのクリア確率を確認することはできない。手順を網羅的に追跡するにはあまりにも場合の数が多すぎるのと、それ以前にこの確認をするのは時間的に不可能である。

そこで、コンピュータシミュレーションを用いて、上海のクリア確率がどの程度のものかを確認することとした。

なお、上海では配牌にある傾向がある。すなわち、頂上牌の下の牌に、同種の牌が来ることが多いということだ。例えば、図１では頂上牌の索１（竹１）の下に筒７（ピン７）が２枚、龍（黒）が２枚配置され、図２では頂上牌の風景の下に、竹２が２枚、風景が１枚配置されている。これ以外にも上海特有の牌の並べ方がある可能性もある。

今回検討のコンピュータシミュレーションにおいては、配牌は全くのランダムとし、実際のゲームにあるような特殊な傾向には配慮しなかった。



コンピュータ・シミュレーションの方法

Excel-VBAによりゲームの成行きを追跡した。方法は次のとおりである。

シミュレーションの方法

ステップ１　乱数を用いて配牌を決定する。Excel上の各カラムには、牌の種類に応じて１～３６の数値が４個ずつ入る。
ステップ２　取り除くことができる牌を選択し、リストを作成する。
ステップ３　そのリストに中よりマッチング可能な牌を２個、乱数を用いて選択する。
ステップ４　選び出された牌を配牌表（Excel上）より取り除き、同時に取り除いた牌の位置と種類を記録する。
ステップ５　ステップ２に還り、同じ手順を繰り返す。取り除けるペアがなくなった時点でゲームの終了となる。

これを図で示すと次の図９となる。

図９　シミュレーションの方法
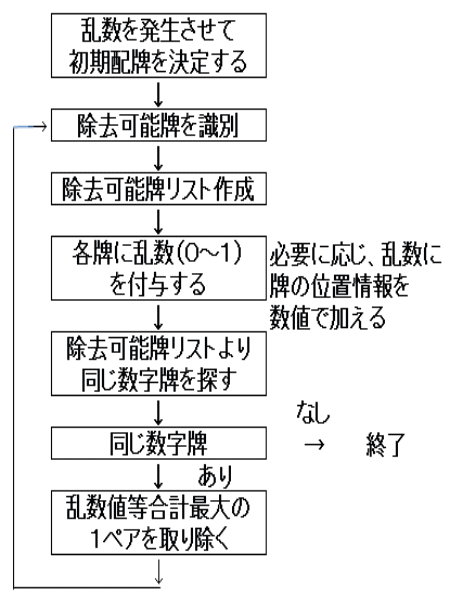	除去可能牌の識別について 　除去可能牌にそれぞれ数値を付して、取り除かれる確率の大きさをコントロールする。付加数値＝乱数値（０～１）＋位置情報値で、位置情報は中央牌＋端牌＋列長さよりなる。 乱数発生について 　除去可能牌が複数種類あり、それらの牌のなかより取り除く２個の牌を決定するために、乱数を用いる。 　例えば、除去可能牌に種類「A」の牌が２個、種類「B」の牌が３個あり、それを識別するために、それぞれの牌に乱数で発生させた０～１の間の数値を付加する。 　たとえば、牌「A1」　0.3、牌「B1」0.5、牌「B2」0.1、牌「A2」0.6、牌「B3」0.7といった具合だ。この場合、A1+A2=0.9、B1+B2=0.6、B1+B3=1.2、B2+B3=0.8となり、合計の一番大きな牌「B1」と牌「B3」を取り除くことにする。	位置情報について 中央牌 　中央に並ぶ牌（図１１のA、B、C、D牌に相当）は、早期に取り除ければ後々のゲームの進展に有利である。そこで、除去可能牌に正の値を付加し、中央牌の取り除かれる確率を高くする。 端牌 　候補牌が取り除かれた時、残った隣の牌上に牌があれば、この残った隣の牌は次の選択では除去可能牌とはならない。残った隣牌上に牌が存在しない場合に正の値を付加し、常に除去可能牌の数が多く保てるようにする。 列長さ 　ある列が長いままゲームの終盤にまで残されていると 、この列に含まれる牌を取り除ける確率が低くなる。長い列に属する候補牌には正の値を付加し、取り除かれる確率を高くする。

実際の上海の配牌より成功確率を求める

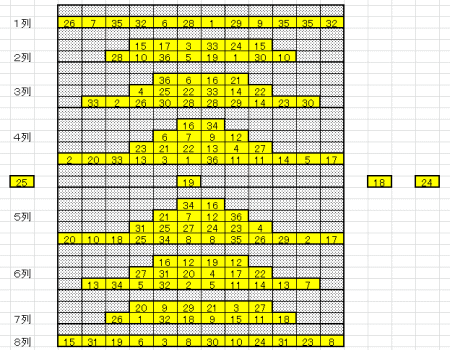
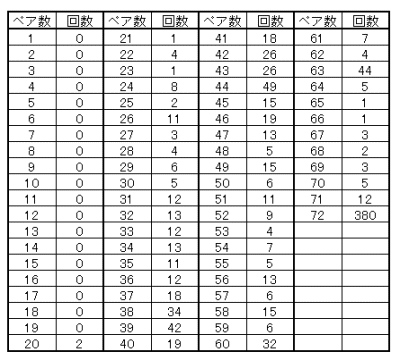
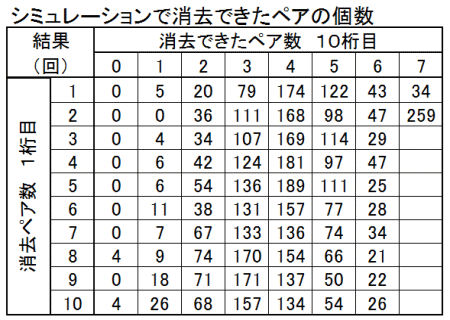
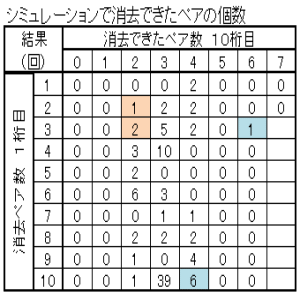
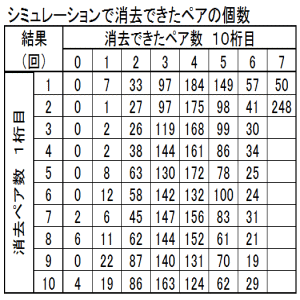
　図１で示した配牌を、図３で示した牌番号に置き換えた。次いで、シミュレーションの方法に示したステップ２～５を繰り返し、１０００回のシミュレーションを行い、そのクリア確率を求めた。図９に示した位置情報は考慮していない。この初期配牌の場合、ランダムに牌を合わせて行っても、クリア確率は３８％と高い値となった。この配牌においてはペア数が３９回、４４回と６３回に高い回数となっているのが特徴的である。

図１０　図１配牌のクリア確率をシミュレーションする	シミュレーション結果　　クリア確率は３８％
初期配牌を牌番号に置き換え、１０００回シミュレーションした	ペア数はゲームオーバーまでに成立したペア数を示し、 　　回数はそのペア数が１０００回のうち何回であったかを示す。

ランダムに作り出した配牌よりクリア確率を求める

　シミュレーションの方法に従い、ステップ１～５を５０００回繰り返し、そのクリア確率を求めた。図９に示した方法は、初期配牌を乱数で発生させ、その配牌がクリアできる確率を求めるフローチャートとなっている。しかし、本シミュレーションにおいては初期配牌を乱数で発生させ、ステップに従ってその配牌がクリアできるかをフローチャートに従って１回だけチャレンジした。この初期配牌の発生から１回のみのチャレンジを５０００回繰り返した。図９に示した位置情報は考慮していない。その結果、クリア確率は５％と低い値であり、ランダムな配牌の決定、そしてランダムなペア合わせではこの程度の数値が妥当なところではないかとの結論である。

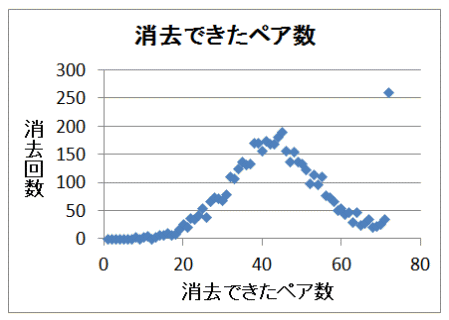
クリア確率を向上させるためには、ゲーム進行の早い段階において、下図１１中の中央牌、A牌、B牌、D牌を早い段階で消去する必要がある。７２ペアが成立すればゲームクリアとなるが、早い段階でA牌、B牌、D牌を取り除けたとしても、４０ペア近辺以降はゲームがクリアできるかどうかは運が支配するところとなっている。

パソコンに入っている上海は、私のような未習熟者が取り組んでもそのクリア確率が２７～２９％であることから、クリア率が上がるように配牌自体に工夫が凝らされていると見るべきであろう。

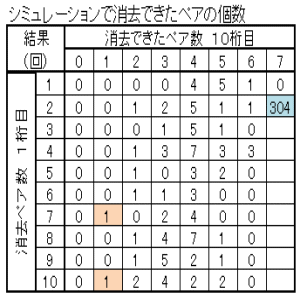
図１１　シミュレーション５０００回繰返し（１回目）　　クリア確率５％
初期配牌を発生させ、どこまでペアが揃うかをみる
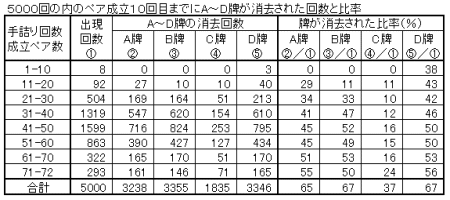
中央牌A～Dが早い機会にクリアできるとゲームがクリアできる確率が高まる。 左下表　A牌、B牌、D牌の３牌が最初の１０ペアの消去に含まれていないと早い機会（３０ペア成立までに）にゲームオーバーとなる確率が高くなる。 右下表　同じく２０ペアまでの消去に含まれていないと、早い機会にゲームオーバーとなる確率が高くなる。ゲームクリアした場合には２０ペアまでにA牌、B牌、D牌が８０％近くの確率で消去されている。
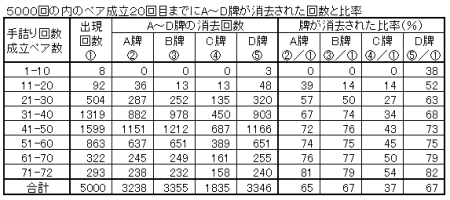※　合計欄は５０００回のゲームオーバー時点でのA牌～D牌の 　　　消去回数を示している。	※　合計欄は５０００回のゲームオーバー時点でのA牌～D牌の 　　　消去回数を示している。

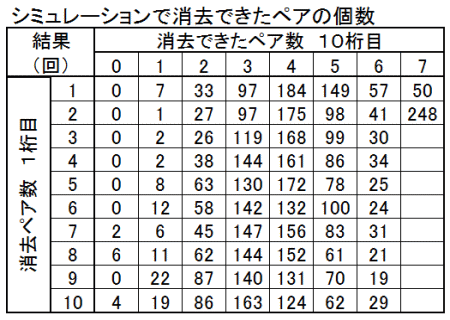
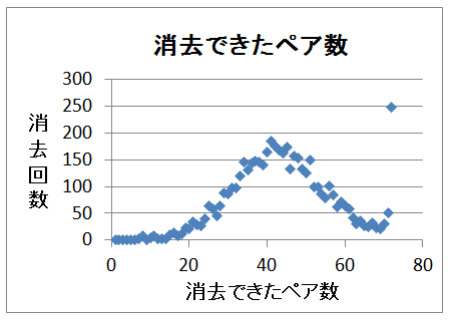
大数の原則を確認する意味でも、再度同じ条件で５０００回シミュレーションを行い、図１２に示すように、図１１に近い結果を得た。

図１２　シミュレーション５０００回繰返し（２回目）　　クリア確率５％
初期配牌を発生させ、どこまでペアが揃うかをみる

ランダムに発生配牌を１００回チャレンジしてみる

図１１および図１２においては、牌の初期配列を乱数で発生させ、その配列について１回限りのチャレンジを行った。それに対して、以下の図１３～図２２に示す結果は、図９のフローシートに従って、与えられた初期配牌について１００回チャレンジした結果を示している。ただし、このシミュレーションにおいては、図９で示した位置情報については考慮していない。全くランダムにペアとなる牌を取り除いた場合の結果を示している。

なお、図１３～図２２に示す初期配牌は、コンピュータ上でランダムに発生させた連続する初期配牌１０ケースをその順番に並べたものである。

初期配牌によっては全くクリアできていないものもあるし、図１６のように１００回のチャレンジ中２０回もクリアできているものもある。図１３から図２２まで各１００回チャレンジしたときのクリア回数は順番に、３回、１回、１回、２０回、０回、１１回、３回、０回、３回、０回となった。この最高となった２０回のクリア率も実際の上海）のクリア率２７～２９％と比べると低いものであるし、図１０で示したように実際の上海の配牌（図１）を同じようにシミュレーションした場合のクリア率３８％と比べるとはるかに低いものである。

図１３から図２２の１０回のクリア率を平均すると４．２％である。これは、図１１での５０００回シミュレーションの５．２％、同じく図１２での５．０％に対しては妥当な数値となっている。ただし、そのばらつきは０回～２０回と非常に大きなものであり、初期配牌にクリア率が大きく影響を受けることを示している。

各ケースについて、良い成績を与えたものから２例、悪い成績を与えたものから２例をとりだし、そのゲームの進行状況を図示した。各ケースの右下にあるリンクをクリックすると各図を表示させることができる。

図１３　Case01　１００回繰返し　クリア確率３％
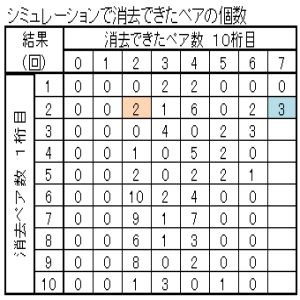	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case01-1　　　Case01-2 上表のピンクの部分 　　　Case01-3　　　Case01-4

図１４　Case0２　１００回繰返し　クリア確率１％
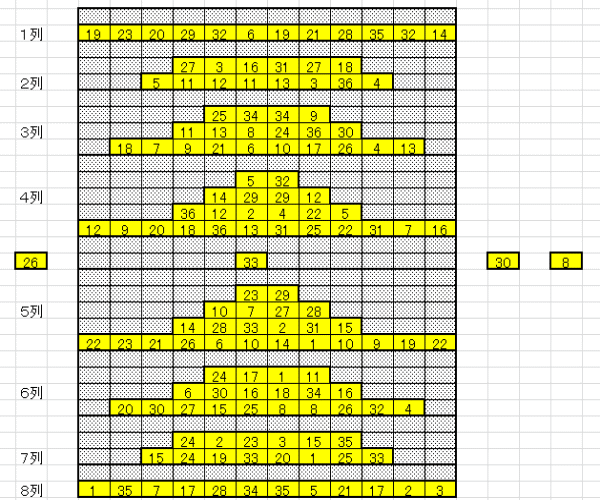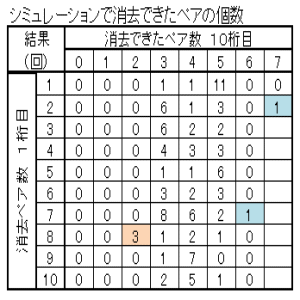	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0２-1　　　Case0２-2 上表のピンクの部分 　　　Case0２-3　　　Case0２-4

図１５　Case0３　１００回繰返し　クリア確率１％
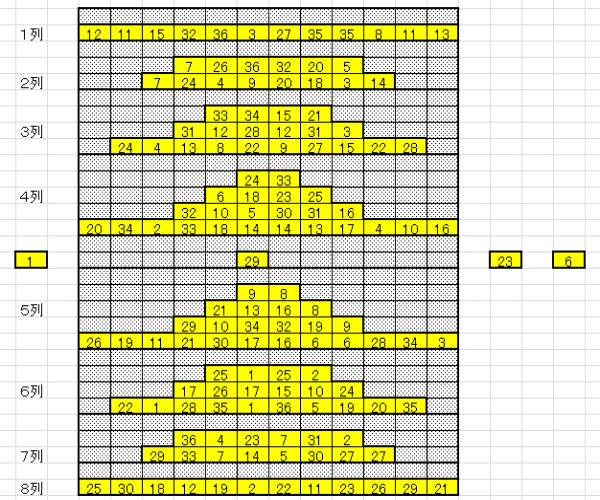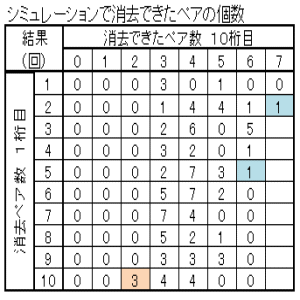	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0３-1　　　Case0３-2 上表のピンクの部分 　　　Case0３-3　　　Case0３-4

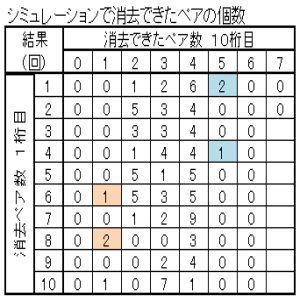
図１６　Case0４　１００回繰返し　クリア確率２０％
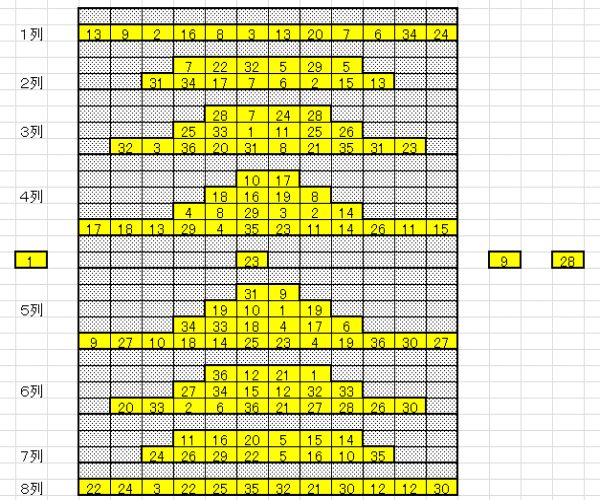	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0４-1　　　Case0４-2 上表のピンクの部分 　　　Case0４-3　　　Case0４-4

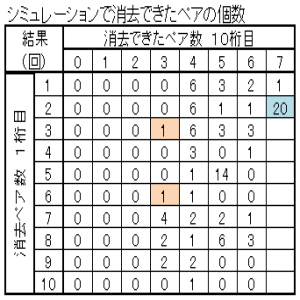
図１７　Case0５　１００回繰返し　クリア確率０％
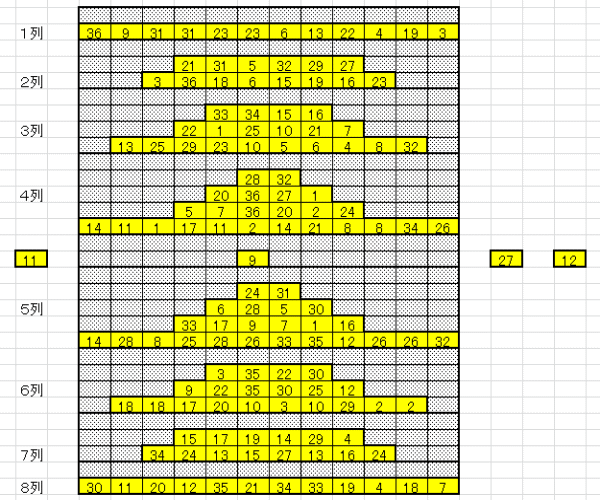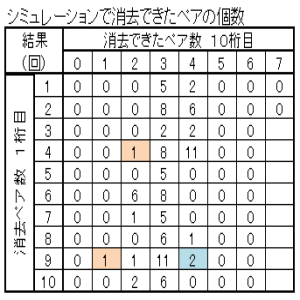	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0５-1　　　Case0５-2 上表のピンクの部分 　　　Case0５-3　　　Case0５-4

図１８　Case0６　１００回繰返し　クリア確率１１％
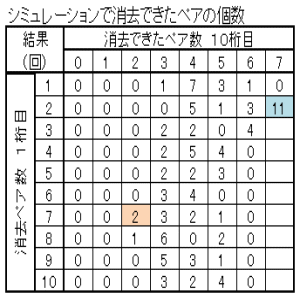	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0６-1　　　Case0６-2 上表のピンクの部分 　　　Case0６-3　　　Case0６-4

図１９　Case0７　１００回繰返し　クリア確率３％
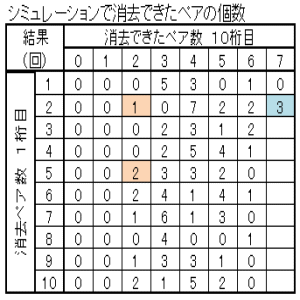	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0７-1　　　Case0７-2 上表のピンクの部分 　　　Case0７-3　　　Case0７-4

図２０　Case0８　１００回繰返し　クリア確率０％
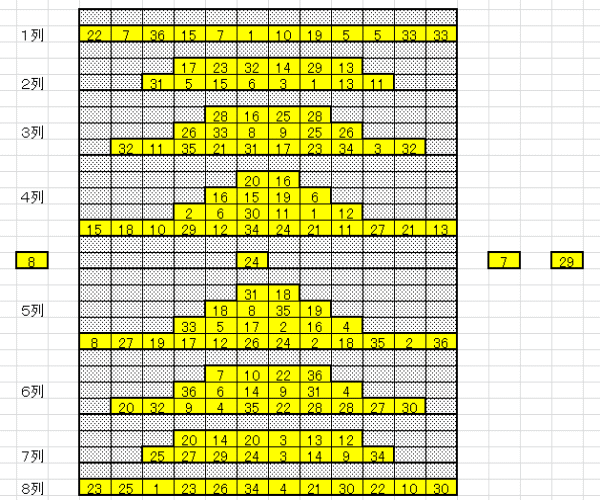	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0８-1　　　Case0８-2 上表のピンクの部分 　　　Case0８-3　　　Case0８-4

図２１　Case0９　１００回繰返し　クリア確率３％
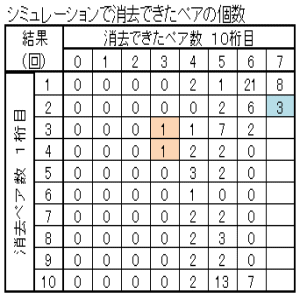	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case0９-1　　　Case0９-2 上表のピンクの部分 　　　Case0９-3　　　Case0９-4

図２２　Case１０　１００回繰返し　クリア確率０％
	消去ペア数の多い方から順に、ペアのマッチングしていく様子を示す。 上表のブルーの部分 　　　Case１０-1　　　Case１０-2 上表のピンクの部分 　　　Case１０-3　　　Case１０-4

位置情報とクリア確率

図９で示した位置情報は、クリア確率に影響を与えると考えられる。そこで、まず、上で示した図１３～図２２のケースについて、１００回中３回のクリア成績を与えたケース１とケース７について、位置情報を変化させてクリア確率がどのように変化するかを確認することにした。

中央　：図９において図１１の牌A～Dが除去可能牌であるとき、その牌に数値情報を加える。
重なり：除去可能牌を取り除いた時に、その横の次に除去可能牌となる牌の上に牌が乗っていない時に数値情報を加える。
長さ　：長い列がそのまま最後まで残るとクリアが難しくなるので、長い列の除去可能牌には大きな数値情報を加える。列長さ／１２０を１単位としている。

結果は、ケース０１の場合を図２３に示した。位置情報を大きくするとクリア確立が向上すると考えたが、逆に小さくなってしまった。むしろ、位置情報をクリアのためには悪い方向と考えられるマイナス値とした場合にクリア確率が向上した。問題個々についてクリアに至る手筋があるということだろう。

ケース０７の場合を図２４に示した。このケースでも位置情報としてプラスの数値を付加するとクリア確率は低下した。

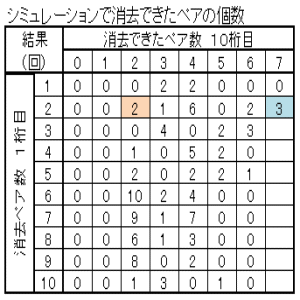
図２３　Case01　　　１００回繰返しシミュレーション当たりのクリア確率と総ペア成立回数
中央-0.1＋重り-0.1＋長さ-0.1＋乱数０～１	中央０＋重なり０＋長さ０＋乱数０～１	中央0.1＋重なり0.1＋長さ0.1＋乱数０～１
クリア確率５％　総ペア成立回数４０７６回	クリア確率３％　総ペア成立回数３９２１回	クリア確率３％　総ペア成立回数４２９７回
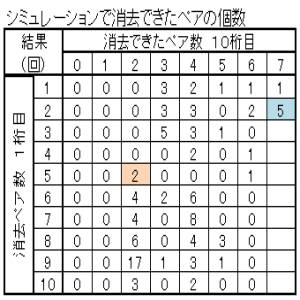中央0.3＋重なり0.2＋長さ0.1＋乱数０～１	中央0.6＋重なり0.4＋長さ0.2＋乱数０～１
クリア確率２％　総ペア成立回数４０４５回	クリア確率０％　総ペア成立回数４３４９回	得られた結果の特徴
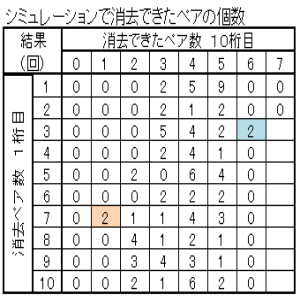		位置情報 ずべてをマイナスにするとクリア率が向上する。
			位置情報 大きくするとよいい方向と思ったが、結果は逆であった。

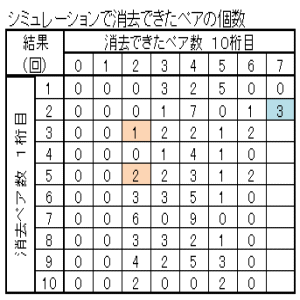
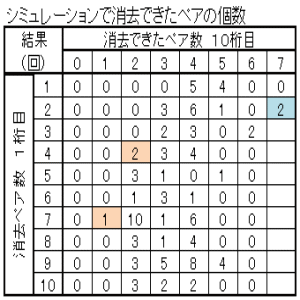
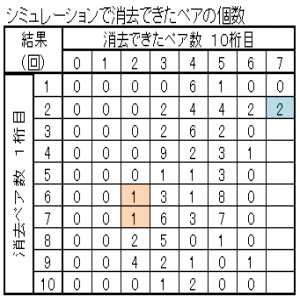
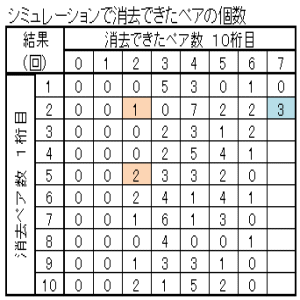
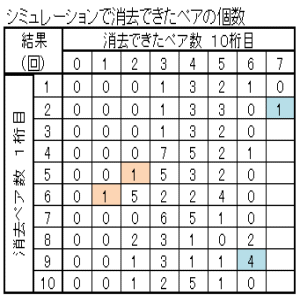
図２４　Case07　　　１００回繰返しシミュレーション当たりのクリア確率と総ペア成立回数
中央-0.1＋重り-0.1＋長さ-0.1＋乱数０～１	中央０＋重なり０＋長さ０＋乱数０～１	中央0.1＋重なり0.1＋長さ0.1＋乱数０～１
クリア確率２％　総ペア成立回数４４７３回	クリア確率３％　総ペア成立回数４４８２回	クリア確率１％　総ペア成立回数４３９８回

５０００回シミュレーションと位置情報

図１１と図１２に示したと同じ方法でシミュレーションを行い、そのクリア確率を調べた。図１１と図１２の位置情報が０のときはそのクリア確率は５．２％と５．０％であったが、位置情報をプラス０．１とするとそのクリア確率はほんの僅かではあるが６．１％へと向上した。下の図２５と図２６を比較してわかるのは、位置情報としてプラス０．１を与えることによって、位置情報がゼロの場合と比較して、低いペア数でゲームオーバーとなる回数が少なくなったということである。

この位置情報をプラス０．３とした時のクリア確率は６．１％となり、位置情報をプラス０．５およびプラス１．０と変化させると、クリア確率は逆に５．３％および５．１％へと低下した。

図２５　図１１の再録	図１２の再録	図２６
中央０＋重なり０＋長さ０＋乱数０～１	中央０＋重なり０＋長さ０＋乱数０～１	中央0.1＋重なり0.1＋長さ0.1＋乱数０～１
クリア確率５％　総ペア成立回数２２４０９３回	クリア確率５％　総ペア成立回数２２３４７８回	クリア確率６％　総ペア成立回数２２８７０１回

麻雀牌の山くずしゲーム上海のクリア確率を上げられるかの結論

最初の配牌によりクリアできるかどうかの確率は大きく変動する。簡単に解ける場合もあるし解くことが不可能な場合もある。

配牌がランダムに行われたとき、ゲームをクリアできる確率は約５％である。

この山崩しに、中央牌はできるだけ早い段階で取り除く配慮をする、除去可能牌の数が多くなるように配慮する、長い列は早く短くするように配慮する、の３つの配慮を行った場合でも、ゲームのクリア確率は無作為に牌を取り除いた場合の５％から６％へと、僅かに１％程度大きくなるのみである。

結論としては、
ゲーム上海で提供されている配牌は約３割の確率で解けることを前提とした配牌である。
解き方に自分流のルールを持ち込んでも、ゲームのクリア確率を著しく向上させることは難しい。
このゲームは囲碁や将棋のような完全情報ゲームではないので、結局は運任せということになるようだ。

ということで、このゲームに時間を費やしても、クリア確率を向上させることは難しいとの結論となった。





　　　　　　　　　　　　　　　　　　　　　　　　　　　ホームページに戻る