Ａ１３　　標準偏差 努力目標 　　理解してください　分散の加法性 技術士試験の問題からは必要最小限の引用にとどめる。（問題）が記されている部分はその引用である。 問題および解答は日本技術士会のホームページより必要に応じて入手してください。 　　技術士第一次試験の問題　　　 問題番号が赤字のものは、ボーナス問題 H２７年　�T−１−５　　　H２１年　�T−１−３　　　H２０年　�T−１−３ H１７年　�T−１−２ 同じ問題 H２７年　�T−１−５　と　H２１年　�T−１−３　と　H１７年　�T−１−２ 関連するブロック Ｅ１５ Ｈ２７年　�T−１−５ 正答：　�@　 （解答） 正規分布は、Ｎ（μ、σ２）と表す。μは平均値、σが標準偏差、σ２が分散である。 Ｎ（μ１、σ１２）とＮ（μ２、σ２２）においてつぎの分散の加法性が成り立つ。 　　　　　　　　　σ２＝σ１２＋σ２２ この問題では、σ２＝０．４２＋０．３２＝０．２５　である。従って、標準偏差σ＝０．５ｍｍとなる。 部材Aと部材Bをつなぎ合わせた３５００ｍｍの結合部品が３５０１．５ｍｍと１．５ｍｍ増える場合、 この１．５ｍｍは３σに相当し（１．５ｍｍ／０．５ｍｍ＝３）、与えられた確率表より結合部材が３５０１．５ｍｍを超える確率は ０．１３％である。 従って答えは�@の０．２％未満となる。 （参考） 正規分布における存在確率は、±１σ以内が６８．３％、±２σ以内が９５．４％、±３σ以内が９９．７％である。この存在確率から外れる分は、正規分布の各々のσ値より低い部分と高い部分である。この問題では高い値３σを超えることを問題としていたので、その超える領域の確率は（１００−９９．７）／２＝０．１５％（与えられている表では０．１３％）となる。 Ｈ２１年　�Tー１−３ 正答：　�A　 （解答） Ｚ=Ｒ−Ｓであるからその平均も　μR−μS 標準偏差は前問と同じく　√（σR2+σS２） H２０年　�T−１−３ この問題はその場で考えていても解けません。 信頼区間とはこのようにして算出するとの公式を覚えましょう。そして、試験会場でこの問題に自信が持てなければパスしましょう。 （解答） （参考） 信頼区間（Ｗｉｋｉｐｅｄｉａ）より抜粋 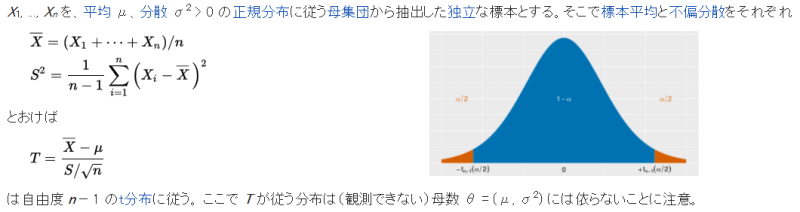Ｈ１７年　�T−１−２ 正答：　なし （解答） 正答なしとなっている。 答えは 　　　（μ、σ2）=[(μ2−μ1)、√(σ12+σ22)] 　　　　　　　　　　　　　　　　問題一覧表へ戻る